Resolvendo problemas da Parte B do Exame Estadual Unificado em matemática
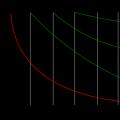
Solução. Os pontos máximos correspondem aos pontos onde o sinal da derivada muda de mais para menos. A figura mostra um gráfico da derivada da função f(x) definida no intervalo (−10; 8). Encontre o número de pontos máximos da função f(x) no intervalo [−9;6].
Solução. Os pontos máximos correspondem aos pontos onde o sinal da derivada muda de mais para menos. No segmento [−9;6] a função tem dois pontos máximos x = − 4 e x = 4. Resposta: 2. A figura mostra um gráfico da derivada da função f(x) definida no intervalo (−10; 8). Encontre o número de pontos máximos da função f(x) no intervalo [−9;6].
Solução. A figura mostra um gráfico da função y=f(x), definida no intervalo (−1; 12). Determine o número de pontos inteiros nos quais a derivada da função é negativa. A derivada de uma função é negativa nos intervalos em que a função diminui.
Solução. A figura mostra um gráfico da função y=f(x), definida no intervalo (−1; 12). Determine o número de pontos inteiros nos quais a derivada da função é negativa. A derivada da função é negativa nos intervalos em que a função diminui, ou seja, nos intervalos (0,5; 3), (6; 10) e (11; 12). Eles contêm pontos inteiros 1, 2, 7, 8 e 9. São 5 pontos no total. Resposta: 5.
A figura mostra um gráfico da derivada da função f(x), definida no intervalo (−10; 4). Encontre os intervalos de diminuição da função f(x). Na sua resposta, indique o comprimento do maior deles. Solução. Os intervalos onde a função f(x) diminui correspondem aos intervalos onde a derivada da função é negativa.
A figura mostra um gráfico da derivada da função f(x), definida no intervalo (−10; 4). Encontre os intervalos de diminuição da função f(x). Na sua resposta, indique o comprimento do maior deles. Solução. Os intervalos decrescentes da função f(x) correspondem aos intervalos em que a derivada da função é negativa, ou seja, o intervalo (−9; −6) de comprimento 3 e o intervalo (−2; 3) de comprimento 5. O comprimento do maior deles é 5. Resposta: 5.
A figura mostra um gráfico da derivada da função f(x) definida no intervalo (−7; 14). Encontre o número de pontos máximos da função f(x) no intervalo [−6; 9]. Solução. Os pontos máximos correspondem aos pontos onde o sinal da derivada muda de positivo para negativo.
A figura mostra um gráfico da derivada da função f(x) definida no intervalo (−7; 14). Encontre o número de pontos máximos da função f(x) no intervalo [−6; 9]. Solução. Os pontos máximos correspondem aos pontos onde o sinal da derivada muda de positivo para negativo. No segmento [−6; 9] a função tem um ponto máximo x = 7. Resposta: 1.
A figura mostra um gráfico da derivada da função f(x), definida no intervalo (−8; 6). Encontre os intervalos de aumento da função f(x). Na sua resposta, indique o comprimento do maior deles. Solução. Os intervalos de aumento da função f(x) correspondem aos intervalos em que a derivada da função é positiva.
A figura mostra um gráfico da derivada da função f(x), definida no intervalo (−8; 6). Encontre os intervalos de aumento da função f(x). Na sua resposta, indique o comprimento do maior deles. Solução. Os intervalos de aumento da função f(x) correspondem aos intervalos em que a derivada da função é positiva, ou seja, os intervalos (−7; −5), (2; 5). O maior deles é o intervalo (2; 5), cujo comprimento é 3.
A figura mostra um gráfico da derivada da função f(x) definida no intervalo (−7; 10). Encontre o número de pontos mínimos da função f(x) no intervalo [−3; 8]. Solução. Os pontos mínimos correspondem aos pontos onde o sinal da derivada muda de menos para mais.
A figura mostra um gráfico da derivada da função f(x) definida no intervalo (−7; 10). Encontre o número de pontos mínimos da função f(x) no intervalo [−3; 8]. Solução. Os pontos mínimos correspondem aos pontos onde o sinal da derivada muda de menos para mais. No segmento [−3; 8] a função tem um ponto mínimo x = 2. Resposta: 1.
A figura mostra um gráfico da derivada da função f(x) definida no intervalo (−16; 4). Encontre o número de pontos extremos da função f(x) no intervalo [−14; 2]. Solução. Os pontos extremos correspondem aos pontos onde o sinal da derivada muda - os zeros da derivada mostrados no gráfico. A derivada desaparece nos pontos −13, −11, −9, −7. No segmento [−14; 2] a função possui 4 pontos extremos. Resposta: 4.
A figura mostra um gráfico da função y=f(x) definida no intervalo (−2; 12). Encontre a soma dos pontos extremos da função f(x). Solução. Função especificada tem máximos nos pontos 1, 4, 9, 11 e mínimos nos pontos 2, 7, 10. Portanto, a soma dos pontos extremos é 1 + 4 + 9 + 11 + 2 + 7 + 10 = 44. Resposta: 44.
A figura mostra um gráfico da função y=f(x) e uma tangente a ela no ponto com a abcissa x 0. Encontre o valor da derivada da função f(x) no ponto x 0 .
A figura mostra um gráfico da função y=f(x) e uma tangente a ela no ponto com a abcissa x 0. Encontre o valor da derivada da função f(x) no ponto x 0 . Solução. O valor da derivada no ponto de tangência é igual à inclinação da tangente, que por sua vez é igual à tangente do ângulo de inclinação desta tangente ao eixo das abcissas. Vamos construir um triângulo com vértices nos pontos A (2; −2), B (2; 0), C (−6; 0). O ângulo de inclinação da tangente ao eixo x será igual ao ângulo adjacente ao ângulo ACB
A figura mostra um gráfico da função y = f(x) e uma tangente a este gráfico no ponto da abcissa igual a 3. Encontre o valor da derivada desta função no ponto x = 3. Para resolver, usamos o significado geométrico da derivada: o valor da derivada da função no ponto é igual à inclinação da tangente ao gráfico desta função desenhado neste ponto. O ângulo tangente é igual à tangente do ângulo entre a tangente e a direção positiva do eixo x (tg α). Ângulo α = β, como ângulos transversais com retas paralelas y=0, y=1 e uma tangente secante. Para o triângulo ABC
A figura mostra o gráfico da função y=f(x) e a tangente a ela no ponto com a abcissa x 0. Encontre o valor da derivada da função f(x) no ponto x 0 .
A figura mostra o gráfico da função y=f(x) e a tangente a ela no ponto com a abcissa x 0. Encontre o valor da derivada da função f(x) no ponto x 0 . De acordo com as propriedades da tangente y=f ′ (x 0)⋅x+b, b=const A figura mostra que a tangente à função f(x) no ponto x 0 passa pelos pontos (-3;2 ), (5,4) . Portanto, podemos criar um sistema de equações
Fontes http://reshuege.ru/
Olá! Vamos chegar ao próximo Exame Estadual Unificado com preparação sistemática de alta qualidade e persistência em moer o granito da ciência!!! EMHá uma tarefa de competição no final do post, seja o primeiro! Em um dos artigos desta seção, você e eu, no qual o gráfico da função foi fornecido, e colocamos várias perguntas relativos a extremos, intervalos de aumento (diminuição) e outros.
Neste artigo, consideraremos os problemas incluídos no Exame de Estado Unificado em matemática, nos quais é dado um gráfico da derivada de uma função e são colocadas as seguintes questões:
1. Em que ponto de um determinado segmento a função assume o maior (ou menor) valor.
2. Encontre o número de pontos máximos (ou mínimos) da função pertencente a um determinado segmento.
3. Encontre o número de pontos extremos da função pertencente a um determinado segmento.
4. Encontre o ponto extremo da função pertencente ao segmento dado.
5. Encontre os intervalos da função crescente (ou decrescente) e na resposta indique a soma dos pontos inteiros incluídos nesses intervalos.
6. Encontre os intervalos de aumento (ou diminuição) da função. Na sua resposta, indique a duração do maior desses intervalos.
7. Encontre o número de pontos nos quais a tangente ao gráfico da função é paralela ou coincide com uma linha da forma y = kx + b.
8. Encontre a abcissa do ponto em que a tangente ao gráfico da função é paralela ao eixo das abcissas ou coincide com ele.
Pode haver outras dúvidas, mas elas não lhe causarão dificuldades se você entender e (são fornecidos links para artigos que fornecem as informações necessárias para a solução, recomendo repeti-los).
Informações básicas (brevemente):
1. A derivada em intervalos crescentes tem sinal positivo.
Se a derivada em um certo ponto de um certo intervalo tiver valor positivo, então o gráfico da função aumenta nesse intervalo.
2. Em intervalos decrescentes, a derivada tem sinal negativo.
Se a derivada em um determinado ponto de um determinado intervalo tiver um valor negativo, então o gráfico da função diminui nesse intervalo.
3. A derivada no ponto x é igual à inclinação da tangente desenhada ao gráfico da função no mesmo ponto.
4. Nos pontos extremos (máximo-mínimo) da função, a derivada é igual a zero. A tangente ao gráfico da função neste ponto é paralela ao eixo x.
Isto deve ser claramente entendido e lembrado!!!
O gráfico derivado “confunde” muitas pessoas. Algumas pessoas inadvertidamente o confundem com o gráfico da própria função. Portanto, em tais edifícios, onde você vê que um gráfico é dado, concentre imediatamente sua atenção na condição no que é dado: o gráfico da função ou o gráfico da derivada da função?
Se for um gráfico da derivada de uma função, trate-o como um “reflexo” da própria função, que simplesmente fornece informações sobre essa função.
Considere a tarefa:
A figura mostra um gráfico você =f'(X)- derivada de uma função f(X), definido no intervalo (–2;21).

Responderemos às seguintes perguntas:
1. Em que ponto do segmento está a função f(X) aceita valor mais alto.
Num determinado intervalo, a derivada de uma função é negativa, o que significa que a função neste intervalo diminui (diminui do limite esquerdo do intervalo para a direita). Assim, o maior valor da função é alcançado na borda esquerda do segmento, ou seja, no ponto 7.
Resposta: 7
2. Em que ponto do segmento está a função f(X)
A partir deste gráfico derivado podemos dizer o seguinte. Num determinado intervalo, a derivada da função é positiva, o que significa que a função neste intervalo aumenta (aumenta do limite esquerdo do intervalo para a direita). Por isso, menor valor a função é alcançada no limite esquerdo do segmento, ou seja, no ponto x = 3.
Resposta: 3
3. Encontre o número de pontos máximos da função f(X)
Os pontos máximos correspondem aos pontos onde o sinal da derivada muda de positivo para negativo. Vamos considerar onde o sinal muda dessa forma.
No segmento (3;6) a derivada é positiva, no segmento (6;16) é negativa.
No segmento (16;18) a derivada é positiva, no segmento (18;20) é negativa.
Assim, em um determinado segmento a função tem dois pontos máximos x = 6 e x = 18.
Resposta: 2
4. Encontre o número de pontos mínimos da função f(X), pertencente ao segmento.
Os pontos mínimos correspondem aos pontos onde o sinal da derivada muda de negativo para positivo. Nossa derivada é negativa no intervalo (0;3) e positiva no intervalo (3;4).
Assim, no segmento a função possui apenas um ponto mínimo x = 3.
*Tenha cuidado ao anotar a resposta - o número de pontos é registrado, e não o valor de x, tal erro pode ser cometido por desatenção;
Resposta 1
5. Encontre o número de pontos extremos da função f(X), pertencente ao segmento.
Observe o que você precisa encontrar quantidade pontos extremos (estes são pontos máximos e mínimos).
Os pontos extremos correspondem aos pontos onde o sinal da derivada muda (de positivo para negativo ou vice-versa). No gráfico dado na condição, esses são os zeros da função. A derivada desaparece nos pontos 3, 6, 16, 18.
Assim, a função possui 4 pontos extremos no segmento.
Resposta: 4
6. Encontre os intervalos da função crescente f(X)
Intervalos de aumento desta função f(X) correspondem aos intervalos em que sua derivada é positiva, ou seja, os intervalos (3;6) e (16;18). Observe que os limites do intervalo não estão incluídos nele (colchetes - os limites não estão incluídos no intervalo, colchetes - incluídos). Esses intervalos contêm pontos inteiros 4, 5, 17. Sua soma é: 4 + 5 + 17 = 26
Resposta: 26
7. Encontre os intervalos da função decrescente f(X) em um determinado intervalo. Na sua resposta, indique a soma dos pontos inteiros incluídos nesses intervalos.
Intervalos decrescentes de função f(X) correspondem a intervalos em que a derivada da função é negativa. Neste problema estes são os intervalos (–2;3), (6;16), (18:21).
Esses intervalos contêm os seguintes pontos inteiros: –1, 0, 1, 2, 7, 8, 9, 10, 11, 12, 13, 14, 15, 19, 20. Sua soma é:
(–1) + 0 + 1 + 2 + 7 + 8 + 9 + 10 +
11 + 12 + 13 + 14 + 15 + 19 + 20 = 140
Resposta: 140
*Preste atenção à condição: se os limites estão incluídos no intervalo ou não. Se os limites forem incluídos, então nos intervalos considerados no processo de solução esses limites também deverão ser levados em consideração.
8. Encontre os intervalos da função crescente f(X)
Intervalos de função crescente f(X) correspondem a intervalos nos quais a derivada da função é positiva. Já os indicamos: (3;6) e (16:18). O maior deles é o intervalo (3;6), seu comprimento é 3.
Resposta: 3
9. Encontre os intervalos da função decrescente f(X). Na sua resposta, indique o comprimento do maior deles.
Intervalos decrescentes de função f(X) correspondem a intervalos em que a derivada da função é negativa. Já os indicamos; estes são os intervalos (–2;3), (6;16), (18;21), seus comprimentos são respectivamente 5, 10, 3.
O comprimento do maior é 10.
Resposta: 10
10. Encontre o número de pontos em que a tangente ao gráfico da função f(X) paralelo ou coincide com a linha reta y = 2x + 3.
O valor da derivada no ponto de tangência é igual à inclinação da tangente. Como a tangente é paralela à reta y = 2x + 3 ou coincide com ela, seus coeficientes angulares são iguais a 2. Isso significa que é necessário encontrar o número de pontos em que y′(x 0) = 2. Geometricamente, isso corresponde ao número de pontos de intersecção do gráfico da derivada com a reta y = 2. Existem 4 desses pontos neste intervalo.
Resposta: 4
11. Encontre o ponto extremo da função f(X), pertencente ao segmento.
O ponto extremo de uma função é o ponto em que sua derivada é igual a zero, e nas proximidades deste ponto a derivada muda de sinal (de positiva para negativa ou vice-versa). No segmento, o gráfico da derivada cruza o eixo x, a derivada muda de sinal de negativo para positivo. Portanto, o ponto x = 3 é um ponto extremo.
Resposta: 3
12. Encontre as abcissas dos pontos em que as tangentes ao gráfico y = f (x) são paralelas ao eixo das abcissas ou coincidem com ele. Na sua resposta, indique o maior deles.
A tangente ao gráfico y = f (x) pode ser paralela ao eixo das abcissas ou coincidir com ele, apenas em pontos onde a derivada é igual a zero (podem ser pontos extremos ou pontos estacionários nas proximidades dos quais a derivada faz não mude seu sinal). Este gráfico mostra que a derivada é zero nos pontos 3, 6, 16,18. O maior é 18.
Você pode estruturar seu raciocínio desta forma:
O valor da derivada no ponto de tangência é igual à inclinação da tangente. Como a tangente é paralela ou coincide com o eixo x, sua inclinação é 0 (na verdade, a tangente de um ângulo de zero grau é zero). Portanto, procuramos o ponto em que a inclinação é igual a zero e, portanto, a derivada é igual a zero. A derivada é igual a zero no ponto em que seu gráfico intercepta o eixo x, e estes são os pontos 3, 6, 16,18.
Resposta: 18
A figura mostra um gráfico você =f'(X)- derivada de uma função f(X), definido no intervalo (–8;4). Em que ponto do segmento [–7;–3] está a função f(X) assume o menor valor.

A figura mostra um gráfico você =f'(X)- derivada de uma função f(X), definido no intervalo (–7;14). Encontre o número de pontos máximos da função f(X), pertencente ao segmento [–6;9].

A figura mostra um gráfico você =f'(X)- derivada de uma função f(X), definido no intervalo (–18;6). Encontre o número de pontos mínimos da função f(X), pertencente ao segmento [–13;1].

A figura mostra um gráfico você =f'(X)- derivada de uma função f(X), definido no intervalo (–11; –11). Encontre o número de pontos extremos da função f(X), pertencente ao segmento [–10; -10].

A figura mostra um gráfico você =f'(X)- derivada de uma função f(X), definido no intervalo (–7;4). Encontre os intervalos da função crescente f(X). Na sua resposta, indique a soma dos pontos inteiros incluídos nesses intervalos.

A figura mostra um gráfico você =f'(X)- derivada de uma função f(X), definido no intervalo (–5;7). Encontre os intervalos da função decrescente f(X). Na sua resposta, indique a soma dos pontos inteiros incluídos nesses intervalos.

A figura mostra um gráfico você =f'(X)- derivada de uma função f(X), definido no intervalo (–11;3). Encontre os intervalos da função crescente f(X). Na sua resposta, indique o comprimento do maior deles.

F A figura mostra um gráfico
As condições do problema são as mesmas (que consideramos). Encontre a soma de três números:
1. A soma dos quadrados dos extremos da função f (x).
2. A diferença entre os quadrados da soma dos pontos máximos e a soma dos pontos mínimos da função f (x).
3. O número de tangentes a f (x) paralelas à linha reta y = –3x + 5.
O primeiro a dar a resposta correta receberá um prêmio de incentivo de 150 rublos. Escreva suas respostas nos comentários. Se este for o seu primeiro comentário no blog, ele não aparecerá imediatamente, mas sim um pouco mais tarde (não se preocupe, o horário em que o comentário foi escrito fica registrado).
Boa sorte para você!
Atenciosamente, Alexander Krutitsikh.
P.S: Ficaria muito grato se você me falasse sobre o site nas redes sociais.
A derivada de uma função é um dos tópicos difíceis em currículo escolar. Nem todo graduado responderá à questão do que é uma derivada.
Este artigo explica de forma simples e clara o que é uma derivada e por que ela é necessária.. Não buscaremos agora o rigor matemático na apresentação. O mais importante é entender o significado.
Vamos lembrar a definição:
A derivada é a taxa de variação de uma função.
A figura mostra gráficos de três funções. Qual você acha que está crescendo mais rápido?
A resposta é óbvia – a terceira. Possui a maior taxa de variação, ou seja, a maior derivada.
Aqui está outro exemplo.
Kostya, Grisha e Matvey conseguiram empregos ao mesmo tempo. Vamos ver como sua renda mudou durante o ano:

O gráfico mostra tudo de uma vez, não é? A renda de Kostya mais que dobrou em seis meses. E a renda de Grisha também aumentou, mas só um pouco. E a renda de Matvey caiu para zero. As condições iniciais são as mesmas, mas a taxa de variação da função, isto é derivado, - diferente. Quanto a Matvey, sua derivada de renda é geralmente negativa.
Intuitivamente, estimamos facilmente a taxa de variação de uma função. Mas como fazemos isso?
O que estamos realmente observando é o quão abruptamente o gráfico de uma função sobe (ou desce). Em outras palavras, com que rapidez y muda à medida que x muda? Obviamente, a mesma função em pontos diferentes pode ter significado diferente derivada - isto é, pode mudar mais rápido ou mais devagar.
A derivada de uma função é denotada por .
Mostraremos como encontrá-lo usando um gráfico.

Um gráfico de alguma função foi desenhado. Vamos pegar um ponto com uma abcissa. Vamos desenhar uma tangente ao gráfico da função neste ponto. Queremos estimar a inclinação do gráfico da função. Um valor conveniente para isso é tangente do ângulo tangente.
A derivada de uma função em um ponto é igual à tangente do ângulo tangente desenhado ao gráfico da função neste ponto.
Observe que como ângulo de inclinação da tangente tomamos o ângulo entre a tangente e a direção positiva do eixo.
Às vezes, os alunos perguntam o que é uma tangente ao gráfico de uma função. Esta é uma linha reta tendo esta área o único ponto comum com o gráfico, e conforme mostrado em nossa figura. Parece uma tangente a um círculo.
Vamos encontrá-lo. Lembramos que a tangente de um ângulo agudo em triângulo retângulo igual à razão entre o lado oposto e o lado adjacente. Do triângulo:
Encontramos a derivada usando um gráfico, mesmo sem conhecer a fórmula da função. Tais problemas são frequentemente encontrados no Exame Estadual Unificado em matemática sob o número.
Existe outra relação importante. Lembre-se de que a reta é dada pela equação
A quantidade nesta equação é chamada inclinação de uma linha reta. É igual à tangente do ângulo de inclinação da reta ao eixo.
.
Nós entendemos isso
Vamos lembrar esta fórmula. Expressa o significado geométrico da derivada.
A derivada de uma função num ponto é igual à inclinação da tangente desenhada ao gráfico da função naquele ponto.
Em outras palavras, a derivada é igual à tangente do ângulo tangente.
Já dissemos que a mesma função pode ter derivadas diferentes em pontos diferentes. Vamos ver como a derivada está relacionada ao comportamento da função.
Vamos desenhar um gráfico de alguma função. Deixe esta função aumentar em algumas áreas e diminuir em outras, e com em velocidades diferentes. E deixe esta função ter pontos de máximo e mínimo.

Num certo ponto a função aumenta. Uma tangente ao gráfico desenhado no ponto forma um ângulo agudo; com direção de eixo positiva. Isso significa que a derivada no ponto é positiva.
Nesse ponto, nossa função diminui. A tangente neste ponto forma um ângulo obtuso; com direção de eixo positiva. Como a tangente de um ângulo obtuso é negativa, a derivada no ponto é negativa.
Aqui está o que acontece:
Se uma função é crescente, sua derivada é positiva.
Se diminuir, sua derivada é negativa.
O que acontecerá nos pontos máximo e mínimo? Vemos que nos pontos (ponto máximo) e (ponto mínimo) a tangente é horizontal. Portanto, a tangente da tangente nesses pontos é zero, e a derivada também é zero.
Ponto - ponto máximo. Neste ponto, o aumento da função é substituído por uma diminuição. Consequentemente, o sinal da derivada muda no ponto “mais” para “menos”.
No ponto - ponto mínimo - a derivada também é zero, mas seu sinal muda de “menos” para “mais”.
Conclusão: utilizando a derivada podemos descobrir tudo o que nos interessa sobre o comportamento de uma função.
Se a derivada for positiva, a função aumenta.
Se a derivada for negativa, a função diminui.
No ponto máximo, a derivada é zero e muda o sinal de “mais” para “menos”.
No ponto mínimo, a derivada também é zero e muda de sinal de “menos” para “mais”.
Vamos escrever essas conclusões em forma de tabela:
| aumenta | ponto máximo | diminui | ponto mínimo | aumenta | |
| + | 0 | - | 0 | + |
Vamos fazer dois pequenos esclarecimentos. Você precisará de um deles para resolver o problema. Outro - no primeiro ano, com um estudo mais sério de funções e derivadas.
É possível que a derivada de uma função em algum ponto seja igual a zero, mas a função não tem máximo nem mínimo neste ponto. Este é o chamado :

Num determinado ponto, a tangente ao gráfico é horizontal e a derivada é zero. Porém, antes do ponto a função aumentou - e depois do ponto continua a aumentar. O sinal da derivada não muda - permanece positivo como estava.
Acontece também que no ponto de máximo ou mínimo a derivada não existe. No gráfico, isso corresponde a uma quebra brusca, quando é impossível traçar uma tangente em um determinado ponto.

Como encontrar a derivada se a função não é dada por um gráfico, mas por uma fórmula? Neste caso aplica-se
A seguir, em sala de aula, é aconselhável considerar uma tarefa fundamental: a partir do gráfico da derivada fornecido, os alunos devem apresentar (claro, com a ajuda do professor) várias questões relacionadas às propriedades da própria função. Naturalmente, essas questões são discutidas, corrigidas se necessário, resumidas, registradas em caderno, após o que se inicia a etapa de resolução dessas tarefas. Aqui é necessário garantir que os alunos não apenas dêem a resposta correta, mas sejam capazes de argumentar (provar), usando as definições, propriedades e regras apropriadas.
Vamos dar um exemplo de tal tarefa: no quadro (por exemplo, usando um projetor), os alunos são apresentados a um gráfico da derivada. 10 tarefas foram formuladas com base nele (questões não totalmente corretas ou duplicadas foram rejeitadas).
A função y = f(x) é definida e contínua no intervalo [–6; 6].
Usando o gráfico da derivada y = f"(x), determine:

1) o número de intervalos da função crescente y = f(x);
2) a duração do intervalo da função decrescente y = f(x);
3) o número de pontos extremos da função y = f(x);
4) ponto máximo da função y = f(x);
5) ponto crítico (estacionário) da função y = f(x), que não é um ponto extremo;
6) a abscissa do ponto do gráfico em que a função y = f(x) assume o maior valor do segmento;
7) a abcissa do ponto do gráfico em que a função y = f(x) assume o menor valor do segmento [–2; 2];
8) o número de pontos no gráfico da função y = f(x), nos quais a tangente é perpendicular ao eixo Oy;
9) o número de pontos no gráfico da função y = f(x), nos quais a tangente forma um ângulo de 60° com o sentido positivo do eixo do Boi;
10) a abscissa do ponto gráfico da função y = f(x), em que a inclinação da tangente assume o menor valor.
Responder: 1) 2; 2) 2; 3) 2; 4) –3; 5) –5; 6) 4; 7) –1; 8) 3; 9) 4; 10) –2.
Para fortalecer as habilidades de estudo das propriedades de uma função, os alunos podem levar para casa uma tarefa relacionada à leitura do mesmo gráfico, mas em um caso é o gráfico de uma função e, no outro, o gráfico de sua derivada.

O artigo foi publicado com o apoio do fórum de administradores de sistemas e programadores. Em "CyberForum.ru" você encontrará fóruns sobre tópicos como programação, computadores, discussões de software, programação web, ciência, eletrônica e Eletrodomésticos, carreira e negócios, recreação, pessoas e sociedade, cultura e arte, casa e família, carros, motocicletas e muito mais. No fórum você pode obter ajuda gratuita. Você pode saber mais no site, localizado em: http://www.cyberforum.ru/diferencial-equations/.
A função y = f(x) é definida e contínua no intervalo [–6; 5]. A imagem mostra:
a) gráfico da função y = f(x);
b) gráfico da derivada y = f"(x).
Determine a partir do cronograma:
1) pontos mínimos da função y = f(x);
2) o número de intervalos da função decrescente y = f(x);
3) a abscissa do ponto do gráfico da função y = f(x), em que assume o maior valor do segmento;
4) o número de pontos no gráfico da função y = f(x), nos quais a tangente é paralela ao eixo do Boi (ou coincide com ele).
Respostas:
a) 1) –3; 2; 4; 2) 3; 3) 3; 4) 4;
b) 1) –2; 4,6;2) 2; 3) 2; 4) 5.
Para realizar o controle, você pode organizar o trabalho em duplas: cada aluno prepara previamente um gráfico de derivada em um cartão para seu parceiro e abaixo oferece 4 a 5 questões para determinar as propriedades da função. Durante as aulas, eles trocam cartões, realizam as tarefas propostas, após o que todos verificam e avaliam o trabalho do parceiro.
A figura mostra um gráfico da derivada da função f(x), definida no intervalo [–5; 6]. Encontre o número de pontos no gráfico de f(x), em cada um dos quais a tangente desenhada ao gráfico da função coincide ou é paralela ao eixo x
A figura mostra um gráfico da derivada da função diferenciável y = f(x).
Encontre o número de pontos no gráfico da função que pertencem ao segmento [–7; 7], em que a tangente ao gráfico da função é paralela à reta especificada pela equação y = –3x.

O ponto material M começa a se mover do ponto A e se move em linha reta por 12 segundos. O gráfico mostra como a distância do ponto A ao ponto M mudou ao longo do tempo. O eixo das abcissas mostra o tempo t em segundos e o eixo das ordenadas mostra a distância s em metros. Determine quantas vezes durante o movimento a velocidade do ponto M chegou a zero (não leve em consideração o início e o fim do movimento).

A figura mostra seções do gráfico da função y=f(x) e a tangente a ela no ponto com a abcissa x = 0. Sabe-se que esta tangente é paralela à reta que passa pelos pontos do gráfico com a abcissa x = -2 e x = 3. Usando isso, encontre o valor da derivada f"(o).

A figura mostra um gráfico de y = f’(x) - a derivada da função f(x), definida no segmento (−11; 2). Encontre a abcissa do ponto em que a tangente ao gráfico da função y = f(x) é paralela ou coincide com a abcissa.

Um ponto material se move retilíneamente de acordo com a lei x(t)=(1/3)t^3-3t^2-5t+3, onde x é a distância do ponto de referência em metros, t é o tempo em segundos, medido desde o início do movimento. Em que momento (em segundos) sua velocidade era igual a 2 m/s?
Um ponto material se move ao longo de uma linha reta da posição inicial até a posição final. A figura mostra um gráfico de seu movimento. O eixo das abcissas mostra o tempo em segundos e o eixo das ordenadas mostra a distância da posição inicial do ponto (em metros). Encontre a velocidade média do ponto. Dê sua resposta em metros por segundo.

A função y = f (x) é definida no intervalo [-4; 4]. A figura mostra um gráfico de sua derivada. Encontre o número de pontos no gráfico da função y = f (x), cuja tangente forma um ângulo de 45° com a direção positiva do eixo do Boi.

A função y = f (x) é definida no intervalo [-2; 4]. A figura mostra um gráfico de sua derivada. Encontre a abcissa do ponto no gráfico da função y = f (x), no qual ela assume o menor valor do segmento [-2; -0,001].

A figura mostra um gráfico da função y = f(x) e uma tangente a este gráfico desenhada no ponto x0. A tangente é dada pela equação y = -2x + 15. Encontre o valor da derivada da função y = -(1/4)f(x) + 5 no ponto x0.

No gráfico da função diferenciável y = f (x) estão marcados sete pontos: x1,.., x7. Encontre todos os pontos marcados nos quais a derivada da função f(x) é maior que zero. Na sua resposta, indique a quantidade desses pontos.

A figura mostra um gráfico y = f"(x) da derivada da função f(x), definida no intervalo (-10; 2). Encontre o número de pontos em que a tangente ao gráfico da função f (x) é paralelo à reta y = -2x-11 ou coincide com ela.

A figura mostra um gráfico de y=f"(x) - a derivada da função f(x). Existem nove pontos marcados no eixo das abcissas: x1, x2, x3, x4, x5, x6, x6, x7, x8, x9.
Quantos desses pontos pertencem aos intervalos da função decrescente f(x)?

A figura mostra um gráfico da função y = f(x) e uma tangente a este gráfico desenhada no ponto x0. A tangente é dada pela equação y = 1,5x + 3,5. Encontre o valor da derivada da função y = 2f(x) - 1 no ponto x0.

A figura mostra o gráfico y=F(x) de um dos funções antiderivadas f(x). Existem seis pontos marcados no gráfico com abcissas x1, x2, ..., x6. Em quantos desses pontos a função y=f(x) assume valores negativos?

A figura mostra um gráfico do carro se movendo ao longo da rota. O eixo das abscissas mostra o tempo (em horas) e o eixo das ordenadas mostra a distância percorrida (em quilômetros). Encontre a velocidade média do carro nesta rota. Dê sua resposta em km/h

Um ponto material se move retilíneamente de acordo com a lei x(t)=(-1/6)t^3+7t^2+6t+1, onde x é a distância do ponto de referência (em metros), t é o tempo de movimento (em segundos). Encontre sua velocidade (em metros por segundo) no instante t = 6 s
A figura mostra um gráfico da antiderivada y = F(x) de alguma função y = f(x), definida no intervalo (-6; 7). Usando a figura, determine o número de zeros da função f(x) neste intervalo.

A figura mostra um gráfico de y = F(x) de uma das antiderivadas de alguma função f(x), definida no intervalo (-7; 5). Usando a figura, determine o número de soluções para a equação f(x) = 0 no intervalo [- 5; 2].

A figura mostra o gráfico da função diferenciável y=f(x). Existem nove pontos marcados no eixo x: x1, x2, ... x9. Encontre todos os pontos marcados nos quais a derivada da função f(x) é negativa. Na sua resposta, indique a quantidade desses pontos.

Um ponto material se move retilíneamente de acordo com a lei x(t)=12t^3−3t^2+2t, onde x é a distância do ponto de referência em metros, t é o tempo em segundos medido desde o início do movimento. Encontre sua velocidade (em metros por segundo) no instante t=6 s.
A figura mostra um gráfico da função y=f(x) e uma tangente a este gráfico desenhada no ponto x0. A equação tangente é mostrada na figura. encontre o valor da derivada da função y=4*f(x)-3 no ponto x0.