વિસ્તારનો ખ્યાલ

કોઈપણ ભૌમિતિક આકૃતિના ક્ષેત્રફળની વિભાવના, ખાસ કરીને ત્રિકોણ, ચોરસ જેવી આકૃતિ સાથે સંકળાયેલ હશે. કોઈપણ ભૌમિતિક આકૃતિના એકમ ક્ષેત્રફળ માટે આપણે ચોરસનો વિસ્તાર લઈશું જેની બાજુ એક સમાન છે. સંપૂર્ણતા માટે, ચાલો વિસ્તારોની વિભાવના માટે બે મૂળભૂત ગુણધર્મોને યાદ કરીએ ભૌમિતિક આકારો.

મિલકત 1:જો ભૌમિતિક આકૃતિઓ સમાન છે, તો તેમના ક્ષેત્રો પણ સમાન છે.

મિલકત 2:કોઈપણ આકૃતિને અનેક આકૃતિઓમાં વિભાજિત કરી શકાય છે. તદુપરાંત, મૂળ આકૃતિનું ક્ષેત્રફળ તેના તમામ ઘટક આકૃતિઓના ક્ષેત્રોના સરવાળા જેટલું છે.

ચાલો એક ઉદાહરણ જોઈએ.

ઉદાહરણ 1

દેખીતી રીતે, ત્રિકોણની એક બાજુ લંબચોરસનો કર્ણ છે, જેની એક બાજુની લંબાઈ $5$ છે (કારણ કે $5$ કોષો છે) અને બીજી $6$ છે (કારણ કે $6$ કોષો છે). તેથી, આ ત્રિકોણનું ક્ષેત્રફળ આવા લંબચોરસના અડધા જેટલું હશે. લંબચોરસનો વિસ્તાર છે

પછી ત્રિકોણનું ક્ષેત્રફળ બરાબર છે

જવાબ: $15$.

આગળ, આપણે ત્રિકોણના ક્ષેત્રો શોધવા માટે ઘણી પદ્ધતિઓનો વિચાર કરીશું, જેમ કે ઊંચાઈ અને આધારનો ઉપયોગ કરીને, હેરોનના સૂત્રનો ઉપયોગ કરીને અને સમભુજ ત્રિકોણનો વિસ્તાર.

ત્રિકોણનો વિસ્તાર તેની ઊંચાઈ અને આધારનો ઉપયોગ કરીને કેવી રીતે શોધવો

પ્રમેય 1

ત્રિકોણનું ક્ષેત્રફળ એક બાજુની લંબાઈ અને તે બાજુની ઊંચાઈના અડધા ગુણાંક તરીકે શોધી શકાય છે.

ગાણિતિક રીતે તે આના જેવું લાગે છે

$S=\frac(1)(2)αh$

જ્યાં $a$ એ બાજુની લંબાઈ છે, $h$ એ તેની તરફ દોરેલી ઊંચાઈ છે.

પુરાવો.

ત્રિકોણ $ABC$ ને ધ્યાનમાં લો જેમાં $AC=α$. ઊંચાઈ $BH$ આ બાજુ દોરવામાં આવે છે, જે $h$ ની બરાબર છે. ચાલો તેને આકૃતિ 2 ની જેમ $AXYC$ ચોરસ સુધી બનાવીએ.

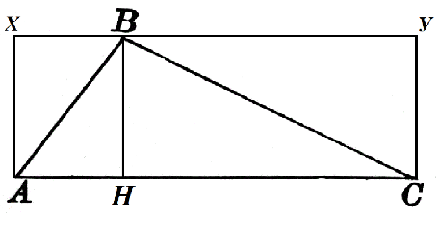
લંબચોરસ $AXBH$ નો વિસ્તાર $h\cdot AH$ છે, અને લંબચોરસ $HBYC$ નો વિસ્તાર $h\cdot HC$ છે. પછી

$S_ABH=\frac(1)(2)h\cdot AH$, $S_CBH=\frac(1)(2)h\cdot HC$

તેથી, ત્રિકોણનું આવશ્યક ક્ષેત્ર, ગુણધર્મ 2 દ્વારા, બરાબર છે

$S=S_ABH+S_CBH=\frac(1)(2)h\cdot AH+\frac(1)(2)h\cdot HC=\frac(1)(2)h\cdot (AH+HC)=\ frac(1)(2)αh$

પ્રમેય સાબિત થયો છે.

ઉદાહરણ 2

જો કોષનો વિસ્તાર એક સમાન હોય તો નીચેની આકૃતિમાં ત્રિકોણનું ક્ષેત્રફળ શોધો

આ ત્રિકોણનો આધાર $9$ બરાબર છે (કારણ કે $9$ $9$ ચોરસ છે). ઊંચાઈ પણ $9$ છે. પછી, પ્રમેય 1 દ્વારા, આપણને મળે છે

$S=\frac(1)(2)\cdot 9\cdot 9=40.5$

જવાબ: $40.5$.

હેરોનનું સૂત્ર

પ્રમેય 2

જો આપણને ત્રિકોણની ત્રણ બાજુઓ $α$, $β$ અને $γ$ આપવામાં આવે, તો તેનો વિસ્તાર નીચે પ્રમાણે શોધી શકાય છે.

$S=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

અહીં $ρ$ એટલે આ ત્રિકોણની અર્ધ-પરિમિતિ.

પુરાવો.

નીચેની આકૃતિ ધ્યાનમાં લો:

પાયથાગોરિયન પ્રમેય દ્વારા, ત્રિકોણમાંથી આપણે $ABH$ મેળવીએ છીએ

ત્રિકોણ $CBH$ થી, પાયથાગોરિયન પ્રમેય મુજબ, આપણી પાસે છે

$h^2=α^2-(β-x)^2$

$h^2=α^2-β^2+2βx-x^2$

આ બે સંબંધોમાંથી આપણને સમાનતા મળે છે

$γ^2-x^2=α^2-β^2+2βx-x^2$

$x=\frac(γ^2-α^2+β^2)(2β)$

$h^2=γ^2-(\frac(γ^2-α^2+β^2)(2β))^2$

$h^2=\frac((α^2-(γ-β)^2)((γ+β)^2-α^2))(4β^2)$

$h^2=\frac((α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α))(4β^2)$

ત્યારથી $ρ=\frac(α+β+γ)(2)$, પછી $α+β+γ=2ρ$, જેનો અર્થ થાય છે

$h^2=\frac(2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α))(4β^2)$

$h^2=\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2 )$

$h=\sqrt(\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2))$

$h=\frac(2)(β)\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

પ્રમેય 1 દ્વારા, આપણે મેળવીએ છીએ

$S=\frac(1)(2) βh=\frac(β)(2)\cdot \frac(2)(β) \sqrt(ρ(ρ-α)(ρ-β)(ρ-γ) )=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

વિરુદ્ધ શિરોબિંદુથી) અને પરિણામી ઉત્પાદનને બે દ્વારા વિભાજીત કરો. આ આના જેવું દેખાય છે:

S = ½ * a * h,

ક્યાં:
S - ત્રિકોણનો વિસ્તાર,
a તેની બાજુની લંબાઈ છે,
h એ આ બાજુથી નીચેની ઊંચાઈ છે.

માપના સમાન એકમોમાં બાજુની લંબાઈ અને ઊંચાઈ રજૂ કરવી આવશ્યક છે. આ કિસ્સામાં, ત્રિકોણનો વિસ્તાર અનુરૂપ “” એકમોમાં મેળવવામાં આવશે.

ઉદાહરણ.
20 સે.મી. લાંબા સ્કેલીન ત્રિકોણની એક બાજુ પર, વિરુદ્ધ શિરોબિંદુમાંથી 10 સે.મી. લાંબો લંબ નીચે આવે છે.
ત્રિકોણનો વિસ્તાર જરૂરી છે.
ઉકેલ.
S = ½ * 20 * 10 = 100 (cm²).

જો સ્કેલેન ત્રિકોણની કોઈપણ બે બાજુઓની લંબાઈ અને તેમની વચ્ચેનો કોણ જાણીતો હોય, તો સૂત્રનો ઉપયોગ કરો:

S = ½ * a * b * sinγ,

જ્યાં: a, b એ બે મનસ્વી બાજુઓની લંબાઈ છે, અને γ એ તેમની વચ્ચેનો ખૂણો છે.

વ્યવહારમાં, ઉદાહરણ તરીકે, જ્યારે માપવા જમીન પ્લોટ, ઉપરોક્ત સૂત્રોનો ઉપયોગ કેટલીકવાર મુશ્કેલ હોય છે, કારણ કે તેમાં વધારાના બાંધકામો અને કોણ માપનની જરૂર પડે છે.

જો તમે સ્કેલેન ત્રિકોણની ત્રણેય બાજુઓની લંબાઈ જાણો છો, તો હેરોનના સૂત્રનો ઉપયોગ કરો:

S = √(p(p-a)(p-b)(p-c)),

a, b, c – ત્રિકોણની બાજુઓની લંબાઈ,
p – અર્ધ-પરિમિતિ: p = (a+b+c)/2.

જો, બધી બાજુઓની લંબાઈ ઉપરાંત, ત્રિકોણમાં અંકિત વર્તુળની ત્રિજ્યા જાણીતી હોય, તો નીચેના કોમ્પેક્ટ સૂત્રનો ઉપયોગ કરો:

જ્યાં: r – અંકિત વર્તુળની ત્રિજ્યા (р – અર્ધ-પરિમિતિ).

સ્કેલેન ત્રિકોણના ક્ષેત્રફળ અને તેની બાજુઓની લંબાઈની ગણતરી કરવા માટે, સૂત્રનો ઉપયોગ કરો:

જ્યાં: R – ઘેરાયેલા વર્તુળની ત્રિજ્યા.

જો તમે ત્રિકોણની એક બાજુની લંબાઈ અને ત્રણ ખૂણા જાણો છો (સૈદ્ધાંતિક રીતે, બે પર્યાપ્ત છે - ત્રીજાનું મૂલ્ય ત્રિકોણના ત્રણ ખૂણાઓના સરવાળાની સમાનતાથી ગણવામાં આવે છે - 180º), તો પછી ઉપયોગ કરો. સૂત્ર:

S = (a² * sinβ * sinγ)/2sinα,

જ્યાં α એ બાજુ a ની વિરુદ્ધ ખૂણાનું મૂલ્ય છે;
β, γ – ત્રિકોણના બાકીના બે ખૂણાઓના મૂલ્યો.

વિસ્તાર સહિત વિવિધ તત્વો શોધવાની જરૂર છે ત્રિકોણ, વિદ્વાન ખગોળશાસ્ત્રીઓમાં ઘણી સદીઓ પૂર્વે દેખાયા હતા પ્રાચીન ગ્રીસ. ચોરસ ત્રિકોણગણતરી કરી શકાય છે વિવિધ રીતેવિવિધ સૂત્રોનો ઉપયોગ કરીને. ગણતરી પદ્ધતિ કયા તત્વો પર આધારિત છે ત્રિકોણજાણીતું

સૂચનાઓ

જો શરતમાંથી આપણે બે બાજુઓ b, c અને તેમના દ્વારા રચાયેલ કોણના મૂલ્યો જાણીએ છીએ?, તો ક્ષેત્રફળ ત્રિકોણ ABC સૂત્ર દ્વારા જોવા મળે છે:
S = (bcsin?)/2.

જો શરતમાંથી આપણે બે બાજુઓ a, b અને તેમના દ્વારા ન બનેલા કોણના મૂલ્યો જાણીએ છીએ?, તો ક્ષેત્રફળ ત્રિકોણ ABC નીચે મુજબ જોવા મળે છે:
કોણ શોધવું?, પાપ? = bsin?/a, પછી કોણ પોતે નક્કી કરવા માટે કોષ્ટકનો ઉપયોગ કરો.
કોણ શોધવું?, ? = 180°-?-?.
આપણે S = (એબ્સિન?)/2 વિસ્તાર પોતે શોધીએ છીએ.

જો સ્થિતિથી આપણે ફક્ત ત્રણ બાજુઓના મૂલ્યો જાણીએ છીએ ત્રિકોણ a, b અને c, પછી વિસ્તાર ત્રિકોણ ABC સૂત્ર દ્વારા જોવા મળે છે:
S = v(p(p-a)(p-b)(p-c)), જ્યાં p અર્ધ-પરિમિતિ p = (a+b+c)/2 છે

જો સમસ્યાની સ્થિતિમાંથી આપણે ઊંચાઈ જાણીએ છીએ ત્રિકોણ h અને જે બાજુ આ ઊંચાઈ ઓછી કરવામાં આવે છે, તે પછી વિસ્તાર ત્રિકોણસૂત્ર અનુસાર ABC:
S = ah(a)/2 = bh(b)/2 = ch(c)/2.

જો આપણે બાજુઓનો અર્થ જાણીએ ત્રિકોણ a, b, c અને આ વિશે વર્ણવેલ ત્રિજ્યા ત્રિકોણઆર, પછી આનો વિસ્તાર ત્રિકોણ ABC સૂત્ર દ્વારા નક્કી કરવામાં આવે છે:
S = abc/4R.
જો ત્રણ બાજુઓ a, b, c અને અંકિતની ત્રિજ્યા જાણીતી હોય, તો ક્ષેત્રફળ ત્રિકોણ ABC સૂત્ર દ્વારા જોવા મળે છે:
S = pr, જ્યાં p એ અર્ધ-પરિમિતિ છે, p = (a+b+c)/2.

જો ABC સમભુજ હોય, તો સૂત્ર દ્વારા વિસ્તાર જોવા મળે છે:
S = (a^2v3)/4.
જો ત્રિકોણ ABC સમદ્વિબાજુ છે, તો ક્ષેત્રફળ સૂત્ર દ્વારા નક્કી કરવામાં આવે છે:
S = (cv(4a^2-c^2))/4, જ્યાં c – ત્રિકોણ.
જો ત્રિકોણ ABC કાટખૂણે હોય, તો ક્ષેત્રફળ સૂત્ર દ્વારા નક્કી થાય છે:
S = ab/2, જ્યાં a અને b પગ છે ત્રિકોણ.
જો ત્રિકોણ ABC એ જમણો સમદ્વિબાજુ ત્રિકોણ છે, તો ક્ષેત્રફળ સૂત્ર દ્વારા નક્કી થાય છે:
S = c^2/4 = a^2/2, જ્યાં c એ કર્ણ છે ત્રિકોણ, a=b – પગ.

વિષય પર વિડિઓ

સ્ત્રોતો:

• ત્રિકોણનું ક્ષેત્રફળ કેવી રીતે માપવું

ટીપ 3: જો કોણ જાણીતું હોય તો ત્રિકોણનું ક્ષેત્રફળ કેવી રીતે શોધવું

વિસ્તાર શોધવા માટે માત્ર એક પરિમાણ (કોણ) જાણવું પૂરતું નથી ટ્રે ચોરસ . જો ત્યાં કોઈ વધારાના પરિમાણો હોય, તો પછી વિસ્તાર નક્કી કરવા માટે તમે સૂત્રોમાંથી એક પસંદ કરી શકો છો જેમાં કોણ મૂલ્ય પણ જાણીતા ચલોમાંના એક તરીકે ઉપયોગમાં લેવાય છે. સૌથી વધુ ઉપયોગમાં લેવાતા કેટલાક સૂત્રો નીચે આપેલ છે.

સૂચનાઓ

જો, બે બાજુઓ દ્વારા રચાયેલા ખૂણા (γ) ના કદ ઉપરાંત ટ્રે ચોરસ , તો પછી આ બાજુઓની લંબાઈ (A અને B) પણ જાણીતી છે ચોરસઆકૃતિના (S) ને બાજુઓની લંબાઈના અડધા ગુણાંક અને આ જાણીતા કોણની સાઈન તરીકે વ્યાખ્યાયિત કરી શકાય છે: S=½×A×B×sin(γ).

જેમ તમને યાદ હશે શાળા અભ્યાસક્રમભૂમિતિ અનુસાર, ત્રિકોણ એ ત્રણ બિંદુઓ દ્વારા જોડાયેલા ત્રણ ભાગોમાંથી બનેલી આકૃતિ છે જે સમાન સીધી રેખા પર નથી. ત્રિકોણ ત્રણ ખૂણા બનાવે છે, તેથી આકૃતિનું નામ. વ્યાખ્યા અલગ હોઈ શકે છે. ત્રિકોણને ત્રણ ખૂણાવાળો બહુકોણ પણ કહી શકાય, જવાબ પણ સાચો હશે. ત્રિકોણને સમાન બાજુઓની સંખ્યા અને આકૃતિઓમાંના ખૂણાઓના કદ અનુસાર વિભાજિત કરવામાં આવે છે. આમ, ત્રિકોણને અનુક્રમે સમદ્વિબાજુ, સમબાજુ અને સ્કેલીન તેમજ લંબચોરસ, તીવ્ર અને સ્થૂળ તરીકે અલગ પાડવામાં આવે છે.

ત્રિકોણના ક્ષેત્રફળની ગણતરી કરવા માટે ઘણા બધા સૂત્રો છે. ત્રિકોણનો વિસ્તાર કેવી રીતે શોધવો તે પસંદ કરો, એટલે કે. કયા ફોર્મ્યુલાનો ઉપયોગ કરવો તે તમારા પર છે. પરંતુ ત્રિકોણના ક્ષેત્રફળની ગણતરી કરવા માટે ઘણા સૂત્રોમાં ઉપયોગમાં લેવાતા કેટલાક સંકેતો જ ધ્યાનમાં લેવા યોગ્ય છે. તેથી, યાદ રાખો:

S એ ત્રિકોણનું ક્ષેત્રફળ છે,

a, b, c ત્રિકોણની બાજુઓ છે,

h એ ત્રિકોણની ઊંચાઈ છે,

R એ ઘેરાયેલા વર્તુળની ત્રિજ્યા છે,

p એ અર્ધ પરિમિતિ છે.

જો તમે તમારો ભૂમિતિ અભ્યાસક્રમ સંપૂર્ણપણે ભૂલી ગયા હોવ તો અહીં મૂળભૂત સંકેતો છે જે તમારા માટે ઉપયોગી થઈ શકે છે. ત્રિકોણના અજાણ્યા અને રહસ્યમય વિસ્તારની ગણતરી કરવા માટે નીચે સૌથી સમજી શકાય તેવા અને જટિલ વિકલ્પો છે. તે મુશ્કેલ નથી અને તમારી ઘરની જરૂરિયાતો માટે અને તમારા બાળકોને મદદ કરવા બંને માટે ઉપયોગી થશે. ચાલો યાદ રાખીએ કે ત્રિકોણના ક્ષેત્રફળની શક્ય તેટલી સરળતાથી ગણતરી કેવી રીતે કરવી:

અમારા કિસ્સામાં, ત્રિકોણનું ક્ષેત્રફળ છે: S = ½ * 2.2 cm * 2.5 cm = 2.75 sq. cm. યાદ રાખો કે વિસ્તાર ચોરસ સેન્ટિમીટર (sqcm) માં માપવામાં આવે છે.

જમણો ત્રિકોણ અને તેનો વિસ્તાર.

જમણો ત્રિકોણ એ એક ત્રિકોણ છે જેમાં એક ખૂણો 90 ડિગ્રી જેટલો હોય છે (તેથી જમણો કહેવાય છે). કાટખૂણો બે લંબ રેખાઓ દ્વારા રચાય છે (ત્રિકોણના કિસ્સામાં, બે લંબ ભાગો). IN જમણો ત્રિકોણત્યાં ફક્ત એક જ કાટકોણ હોઈ શકે છે, કારણ કે કોઈપણ એક ત્રિકોણના તમામ ખૂણાઓનો સરવાળો 180 ડિગ્રી જેટલો છે. તે તારણ આપે છે કે અન્ય 2 ખૂણાઓએ બાકીની 90 ડિગ્રી શેર કરવી જોઈએ, ઉદાહરણ તરીકે 70 અને 20, 45 અને 45, વગેરે. તેથી, તમને મુખ્ય વસ્તુ યાદ છે, જે બાકી છે તે શોધવાનું છે કે સમકોણ ત્રિકોણનો વિસ્તાર કેવી રીતે શોધવો. ચાલો કલ્પના કરીએ કે આપણી સામે આવો કાટકોણ ત્રિકોણ છે, અને આપણે તેનો વિસ્તાર S શોધવાની જરૂર છે.

1. કાટકોણ ત્રિકોણનું ક્ષેત્રફળ નક્કી કરવાની સૌથી સરળ રીત નીચેના સૂત્રનો ઉપયોગ કરીને ગણવામાં આવે છે:

અમારા કિસ્સામાં, જમણા ત્રિકોણનું ક્ષેત્રફળ છે: S = 2.5 cm * 3 cm/2 = 3.75 sq. cm.

સૈદ્ધાંતિક રીતે, ત્રિકોણના ક્ષેત્રને અન્ય રીતે ચકાસવાની હવે કોઈ જરૂર નથી, કારણ કે ફક્ત આ જ ઉપયોગી થશે અને રોજિંદા જીવનમાં મદદ કરશે. પરંતુ તીવ્ર ખૂણા દ્વારા ત્રિકોણના વિસ્તારને માપવા માટેના વિકલ્પો પણ છે.

2. અન્ય ગણતરી પદ્ધતિઓ માટે, તમારી પાસે કોસાઇન, સાઇન અને ટેન્જેન્ટનું કોષ્ટક હોવું આવશ્યક છે. તમારા માટે ન્યાયાધીશ, અહીં કાટકોણ ત્રિકોણના ક્ષેત્રફળની ગણતરી માટેના કેટલાક વિકલ્પો છે જેનો ઉપયોગ હજી પણ થઈ શકે છે:

અમે પ્રથમ સૂત્રનો ઉપયોગ કરવાનું નક્કી કર્યું અને કેટલાક નાના ફોલ્લીઓ સાથે (અમે તેને એક નોટબુકમાં દોર્યું અને જૂના શાસક અને પ્રોટ્રેક્ટરનો ઉપયોગ કર્યો), પરંતુ અમને સાચી ગણતરી મળી:

S = (2.5*2.5)/(2*0.9)=(3*3)/(2*1.2). અમને નીચેના પરિણામો મળ્યા: 3.6 = 3.7, પરંતુ કોષોની પાળીને ધ્યાનમાં લેતા, અમે આ ઉપદ્રવને માફ કરી શકીએ છીએ.

સમદ્વિબાજુ ત્રિકોણ અને તેનો વિસ્તાર.

જો તમને સમદ્વિબાજુ ત્રિકોણ માટે સૂત્રની ગણતરી કરવાના કાર્યનો સામનો કરવો પડી રહ્યો છે, તો સૌથી સહેલો રસ્તો એ છે કે મુખ્ય અને ત્રિકોણના ક્ષેત્રફળ માટે જે શાસ્ત્રીય સૂત્ર માનવામાં આવે છે તેનો ઉપયોગ કરવો.

પરંતુ પહેલા, સમદ્વિબાજુ ત્રિકોણનું ક્ષેત્રફળ શોધતા પહેલા, ચાલો જાણી લઈએ કે તે કયા પ્રકારની આકૃતિ છે. સમદ્વિબાજુ ત્રિકોણ એક ત્રિકોણ છે જેમાં બે બાજુઓની લંબાઈ સમાન હોય છે. આ બે બાજુઓને બાજુની કહેવામાં આવે છે, ત્રીજી બાજુને આધાર કહેવામાં આવે છે. સમબાજુ ત્રિકોણને સમબાજુ ત્રિકોણ સાથે મૂંઝવશો નહીં, એટલે કે. ત્રણેય બાજુઓ સમાન ધરાવતો નિયમિત ત્રિકોણ. આવા ત્રિકોણમાં ખૂણાઓ અથવા તેના કદમાં કોઈ વિશેષ વલણ નથી. જો કે, સમદ્વિબાજુ ત્રિકોણમાં આધાર પરના ખૂણા સમાન હોય છે, પરંતુ સમાન બાજુઓ વચ્ચેના ખૂણાથી અલગ હોય છે. તેથી, તમે પહેલાથી જ પ્રથમ અને મુખ્ય સૂત્ર જાણો છો; સમદ્વિબાજુ ત્રિકોણનું ક્ષેત્રફળ નક્કી કરવા માટેના અન્ય કયા સૂત્રો જાણીતા છે તે શોધવાનું બાકી છે:

ત્રિકોણ એ સૌથી સામાન્ય ભૌમિતિક આકારોમાંનું એક છે, જેનાથી આપણે પહેલાથી જ પરિચિત થઈએ છીએ પ્રાથમિક શાળા. દરેક વિદ્યાર્થીને ભૂમિતિના પાઠમાં ત્રિકોણનો વિસ્તાર કેવી રીતે શોધવો તે પ્રશ્નનો સામનો કરવો પડે છે. તો, આપેલ આકૃતિનું ક્ષેત્રફળ શોધવાની કઈ વિશેષતાઓ ઓળખી શકાય? આ લેખમાં આપણે આવા કાર્યને પૂર્ણ કરવા માટે જરૂરી મૂળભૂત સૂત્રો જોઈશું અને ત્રિકોણના પ્રકારોનું પણ વિશ્લેષણ કરીશું.

ત્રિકોણના પ્રકાર

તમે ત્રિકોણનો વિસ્તાર એકદમ શોધી શકો છો અલગ અલગ રીતે, કારણ કે ભૂમિતિમાં ત્રણ ખૂણાઓ ધરાવતી એક કરતાં વધુ પ્રકારની આકૃતિઓ છે. આ પ્રકારોમાં શામેલ છે:

• સ્થૂળ.
• સમભુજ (સાચો).
• જમણો ત્રિકોણ.
• સમદ્વિબાજુ.

ચાલો તેમને દરેક પર નજીકથી નજર કરીએ હાલના પ્રકારોત્રિકોણ

ભૌમિતિક સમસ્યાઓ હલ કરતી વખતે આ ભૌમિતિક આકૃતિને સૌથી સામાન્ય ગણવામાં આવે છે. જ્યારે મનસ્વી ત્રિકોણ દોરવાની જરૂરિયાત ઊભી થાય છે, ત્યારે આ વિકલ્પ બચાવમાં આવે છે.

તીવ્ર ત્રિકોણમાં, નામ સૂચવે છે તેમ, બધા ખૂણા તીવ્ર હોય છે અને 180° સુધી ઉમેરે છે.

આ પ્રકારનો ત્રિકોણ પણ ખૂબ જ સામાન્ય છે, પરંતુ તીવ્ર ત્રિકોણ કરતાં થોડો ઓછો સામાન્ય છે. ઉદાહરણ તરીકે, ત્રિકોણ હલ કરતી વખતે (એટલે ​​કે, તેની ઘણી બાજુઓ અને ખૂણાઓ જાણીતા છે અને તમારે બાકીના તત્વો શોધવાની જરૂર છે), કેટલીકવાર તમારે કોણ સ્થૂળ છે કે નહીં તે નક્કી કરવાની જરૂર છે. કોસાઇન એ નકારાત્મક સંખ્યા છે.

B, એક ખૂણાનું મૂલ્ય 90° કરતાં વધી જાય છે, તેથી બાકીના બે ખૂણા નાના મૂલ્યો લઈ શકે છે (ઉદાહરણ તરીકે, 15° અથવા તો 3°).

આ પ્રકારના ત્રિકોણનું ક્ષેત્રફળ શોધવા માટે, તમારે કેટલીક ઘોંઘાટ જાણવાની જરૂર છે, જેના વિશે આપણે પછીથી વાત કરીશું.

નિયમિત અને સમદ્વિબાજુ ત્રિકોણ

નિયમિત બહુકોણ એ એક આકૃતિ છે જેમાં n ખૂણાઓ શામેલ છે અને બધી બાજુઓ અને ખૂણાઓ સમાન છે. આ એક નિયમિત ત્રિકોણ છે. ત્રિકોણના તમામ ખૂણાઓનો સરવાળો 180° હોવાથી, ત્રણેય ખૂણોમાંથી દરેક 60° છે.

નિયમિત ત્રિકોણ, તેની મિલકતને કારણે, તેને સમભુજ આકૃતિ પણ કહેવામાં આવે છે.

તે નોંધવું પણ યોગ્ય છે કે નિયમિત ત્રિકોણમાં ફક્ત એક વર્તુળ લખી શકાય છે, અને તેની આસપાસ ફક્ત એક વર્તુળનું વર્ણન કરી શકાય છે, અને તેમના કેન્દ્રો એક જ બિંદુ પર સ્થિત છે.

સમબાજુના પ્રકાર ઉપરાંત, કોઈ સમદ્વિબાજુ ત્રિકોણને પણ અલગ કરી શકે છે, જે તેનાથી થોડો અલગ છે. આવા ત્રિકોણમાં, બે બાજુઓ અને બે ખૂણા એકબીજાની સમાન હોય છે, અને ત્રીજી બાજુ (જેની બાજુમાં સમાન ખૂણા હોય છે) એ આધાર છે.

આકૃતિ એક સમદ્વિબાજુ ત્રિકોણ DEF દર્શાવે છે જેના ખૂણા D અને F સમાન છે અને DF આધાર છે.

જમણો ત્રિકોણ

કાટકોણ ત્રિકોણનું નામ એટલા માટે રાખવામાં આવ્યું છે કારણ કે તેનો એક ખૂણો જમણો છે, એટલે કે 90° બરાબર છે. અન્ય બે ખૂણાઓ 90° સુધી ઉમેરે છે.

આવા ત્રિકોણની સૌથી મોટી બાજુ, 90° કોણની સામે પડેલી છે, તે કર્ણ છે, જ્યારે બાકીની બે બાજુઓ પગ છે. આ પ્રકારના ત્રિકોણ માટે, પાયથાગોરિયન પ્રમેય લાગુ પડે છે:

પગની લંબાઈના ચોરસનો સરવાળો કર્ણોની લંબાઈના વર્ગના બરાબર છે.

આકૃતિ AC અને પગ AB અને BC સાથે કાટકોણ ત્રિકોણ BAC દર્શાવે છે.

કાટકોણવાળા ત્રિકોણનું ક્ષેત્રફળ શોધવા માટે, તમારે તેના પગના આંકડાકીય મૂલ્યો જાણવાની જરૂર છે.

ચાલો આપેલ આકૃતિનું ક્ષેત્રફળ શોધવા માટેના સૂત્રો તરફ આગળ વધીએ.

વિસ્તાર શોધવા માટે મૂળભૂત સૂત્રો

ભૂમિતિમાં, બે સૂત્રોને ઓળખી શકાય છે જે મોટાભાગના પ્રકારના ત્રિકોણનો વિસ્તાર શોધવા માટે યોગ્ય છે, જેમ કે તીવ્ર, સ્થૂળ, નિયમિત અને સમદ્વિબાજુ ત્રિકોણ. ચાલો તેમાંના દરેકને જોઈએ.

બાજુ અને ઊંચાઈ દ્વારા

આ સૂત્ર આપણે વિચારી રહ્યા છીએ તે આકૃતિનું ક્ષેત્રફળ શોધવા માટે સાર્વત્રિક છે. આ કરવા માટે, બાજુની લંબાઈ અને તેના તરફ દોરવામાં આવેલી ઊંચાઈની લંબાઈ જાણવા માટે તે પૂરતું છે. સૂત્ર પોતે (બેઝ અને ઊંચાઈનું અડધું ઉત્પાદન) નીચે મુજબ છે:

જ્યાં A એ આપેલ ત્રિકોણની બાજુ છે અને H એ ત્રિકોણની ઊંચાઈ છે.

ઉદાહરણ તરીકે, તીવ્ર ત્રિકોણ ACB નો વિસ્તાર શોધવા માટે, તમારે તેની બાજુ AB ને ઊંચાઈ CD વડે ગુણાકાર કરવાની અને પરિણામી મૂલ્યને બે વડે વિભાજીત કરવાની જરૂર છે.

જો કે, આ રીતે ત્રિકોણનું ક્ષેત્રફળ શોધવું હંમેશા સરળ હોતું નથી. ઉદાહરણ તરીકે, સ્થૂળ ત્રિકોણ માટે આ સૂત્રનો ઉપયોગ કરવા માટે, તમારે તેની એક બાજુ લંબાવવાની જરૂર છે અને તે પછી જ તેની ઉપર ઊંચાઈ દોરો.

વ્યવહારમાં, આ સૂત્રનો ઉપયોગ અન્ય કરતા વધુ વખત થાય છે.

બંને બાજુઓ અને ખૂણા પર

આ સૂત્ર, અગાઉના એકની જેમ, મોટાભાગના ત્રિકોણ માટે યોગ્ય છે અને તેના અર્થમાં ત્રિકોણની બાજુ અને ઊંચાઈનો વિસ્તાર શોધવા માટેના સૂત્રનું પરિણામ છે. એટલે કે, પ્રશ્નમાંનું સૂત્ર અગાઉના સૂત્રમાંથી સરળતાથી મેળવી શકાય છે. તેની રચના આના જેવી લાગે છે:

S = ½*sinO*A*B,

જ્યાં A અને B ત્રિકોણની બાજુઓ છે અને O એ A અને B બાજુઓ વચ્ચેનો ખૂણો છે.

ચાલો યાદ કરીએ કે ઉત્કૃષ્ટ સોવિયેત ગણિતશાસ્ત્રી વી.એમ. બ્રાડિસના નામ પરથી એક વિશિષ્ટ કોષ્ટકમાં કોણની સાઈન જોઈ શકાય છે.

હવે ચાલો અન્ય સૂત્રો તરફ આગળ વધીએ જે ફક્ત અસાધારણ પ્રકારના ત્રિકોણ માટે યોગ્ય છે.

કાટકોણ ત્રિકોણનું ક્ષેત્રફળ

સાર્વત્રિક સૂત્ર ઉપરાંત, જેમાં ત્રિકોણમાં ઊંચાઈ શોધવાની જરૂરિયાતનો સમાવેશ થાય છે, જમણો ખૂણો ધરાવતા ત્રિકોણનો વિસ્તાર તેના પગમાંથી શોધી શકાય છે.

આમ, જમણો ખૂણો ધરાવતા ત્રિકોણનું ક્ષેત્રફળ તેના પગનું અડધું ઉત્પાદન છે, અથવા:

જ્યાં a અને b કાટકોણ ત્રિકોણના પગ છે.

નિયમિત ત્રિકોણ

આ પ્રકારભૌમિતિક આકૃતિઓ અલગ પડે છે કે તેનો વિસ્તાર તેની માત્ર એક બાજુના દર્શાવેલ મૂલ્ય સાથે મળી શકે છે (કારણ કે નિયમિત ત્રિકોણની બધી બાજુઓ સમાન હોય છે). તેથી, જ્યારે "જ્યારે બાજુઓ સમાન હોય ત્યારે ત્રિકોણનો વિસ્તાર શોધવા" ના કાર્યનો સામનો કરવામાં આવે ત્યારે તમારે નીચેના સૂત્રનો ઉપયોગ કરવાની જરૂર છે:

S = A 2 *√3 / 4,

જ્યાં A એ સમબાજુ ત્રિકોણની બાજુ છે.

હેરોનનું સૂત્ર

ત્રિકોણનું ક્ષેત્રફળ શોધવાનો છેલ્લો વિકલ્પ હેરોનનું સૂત્ર છે. તેનો ઉપયોગ કરવા માટે, તમારે આકૃતિની ત્રણ બાજુઓની લંબાઈ જાણવાની જરૂર છે. હેરોનનું સૂત્ર આના જેવું લાગે છે:

S = √p·(p - a)·(p - b)·(p - c),

જ્યાં a, b અને c આપેલ ત્રિકોણની બાજુઓ છે.

કેટલીકવાર સમસ્યા આપવામાં આવે છે: "નિયમિત ત્રિકોણનો વિસ્તાર તેની બાજુની લંબાઈ શોધવા માટે છે." IN આ કિસ્સામાંઆપણે નિયમિત ત્રિકોણનું ક્ષેત્રફળ શોધવા માટે આપણે પહેલાથી જ જાણીએ છીએ તે સૂત્રનો ઉપયોગ કરવાની જરૂર છે અને તેમાંથી બાજુનું મૂલ્ય (અથવા તેના ચોરસ) મેળવવાની જરૂર છે:

A 2 = 4S / √3.

પરીક્ષા કાર્યો

ગણિતમાં GIA સમસ્યાઓના ઘણા સૂત્રો છે. વધુમાં, ઘણી વાર ચેકર્ડ કાગળ પર ત્રિકોણનું ક્ષેત્રફળ શોધવાનું જરૂરી છે.

આ કિસ્સામાં, આકૃતિની એક બાજુએ ઊંચાઈ દોરવી, કોષોમાંથી તેની લંબાઈ નક્કી કરવી અને તેનો ઉપયોગ કરવો સૌથી અનુકૂળ છે. સાર્વત્રિક સૂત્રવિસ્તાર શોધવા માટે:

તેથી, લેખમાં પ્રસ્તુત સૂત્રોનો અભ્યાસ કર્યા પછી, તમને કોઈપણ પ્રકારના ત્રિકોણનું ક્ષેત્રફળ શોધવામાં કોઈ સમસ્યા નહીં થાય.

ત્રિકોણનું ક્ષેત્રફળ - સૂત્રો અને સમસ્યા હલ કરવાના ઉદાહરણો

નીચે છે મનસ્વી ત્રિકોણનું ક્ષેત્રફળ શોધવા માટેના સૂત્રોજે કોઈપણ ત્રિકોણનો વિસ્તાર શોધવા માટે યોગ્ય છે, તેના ગુણધર્મો, ખૂણા અથવા કદને ધ્યાનમાં લીધા વિના. સૂત્રો તેમની અરજી માટેના સ્પષ્ટીકરણો અથવા તેમની સાચીતા માટેના સમર્થન સાથે ચિત્રના સ્વરૂપમાં રજૂ કરવામાં આવે છે. ઉપરાંત, એક અલગ આકૃતિ ફોર્મ્યુલામાં અક્ષર પ્રતીકો અને ડ્રોઇંગમાં ગ્રાફિક પ્રતીકો વચ્ચેનો પત્રવ્યવહાર દર્શાવે છે.

નોંધ . જો ત્રિકોણમાં વિશેષ ગુણધર્મો છે (સમદ્વિબાજુ, લંબચોરસ, સમભુજ), તો તમે નીચે આપેલા સૂત્રોનો ઉપયોગ કરી શકો છો, તેમજ વધારાના વિશેષ સૂત્રોનો ઉપયોગ કરી શકો છો જે ફક્ત આ ગુણધર્મોવાળા ત્રિકોણ માટે માન્ય છે:

• "એક સમભુજ ત્રિકોણના ક્ષેત્રફળ માટેના સૂત્રો"

ત્રિકોણ ક્ષેત્રના સૂત્રો

સૂત્રો માટે સ્પષ્ટતા:
a, b, c- ત્રિકોણની બાજુઓની લંબાઈ જેનો વિસ્તાર આપણે શોધવા માંગીએ છીએ
આર- ત્રિકોણમાં અંકિત વર્તુળની ત્રિજ્યા
આર- ત્રિકોણની ફરતે ઘેરાયેલ વર્તુળની ત્રિજ્યા
h- ત્રિકોણની ઊંચાઈ બાજુથી ઓછી થઈ
પી- ત્રિકોણની અર્ધ-પરિમિતિ, તેની બાજુઓનો સરવાળો 1/2 (પરિમિતિ)
α - ત્રિકોણની બાજુ a ની વિરુદ્ધ કોણ
β - ત્રિકોણની બાજુ b ની વિરુદ્ધ કોણ
γ - ત્રિકોણની બાજુ c ની વિરુદ્ધ કોણ
h a, h b , h c- ત્રિકોણની ઊંચાઈ બાજુઓ a, b, c સુધી નીચી

મહેરબાની કરીને નોંધ કરો કે આપેલ સંકેતો ઉપરની આકૃતિને અનુરૂપ છે, જેથી કરીને વાસ્તવિક ભૂમિતિની સમસ્યા હલ કરતી વખતે, તમારા માટે સૂત્રમાં યોગ્ય સ્થાનો પર યોગ્ય મૂલ્યોને બદલવાનું દૃષ્ટિની રીતે સરળ બનશે.

• ત્રિકોણનો વિસ્તાર છે ત્રિકોણની ઊંચાઈનો અડધો ગુણાંક અને બાજુની લંબાઈ જેના દ્વારા આ ઊંચાઈ ઓછી કરવામાં આવે છે(સૂત્ર 1). આ સૂત્રની સાચીતા તાર્કિક રીતે સમજી શકાય છે. પાયાની નીચેની ઊંચાઈ મનસ્વી ત્રિકોણને બે લંબચોરસમાં વિભાજિત કરશે. જો તમે તેમાંથી દરેકને b અને h પરિમાણ સાથે લંબચોરસમાં બાંધો છો, તો દેખીતી રીતે આ ત્રિકોણનું ક્ષેત્રફળ લંબચોરસના બરાબર અડધા ક્ષેત્રફળ (Spr = bh) જેટલું હશે.
• ત્રિકોણનો વિસ્તાર છે તેની બે બાજુઓનો અડધો ગુણાંક અને તેમની વચ્ચેના ખૂણાની સાઈન(સૂત્ર 2) (નીચે આ સૂત્રનો ઉપયોગ કરીને સમસ્યા હલ કરવાનું ઉદાહરણ જુઓ). હકીકત એ છે કે તે પાછલા એક કરતા અલગ લાગે છે છતાં, તે સરળતાથી તેમાં રૂપાંતરિત થઈ શકે છે. જો આપણે કોણ B થી બાજુ b સુધીની ઊંચાઈ ઓછી કરીએ, તો તે તારણ આપે છે કે બાજુ a નું ઉત્પાદન અને કોણ γ ની સાઈન, કાટકોણ ત્રિકોણમાં સાઈનના ગુણધર્મો અનુસાર, આપણે દોરેલા ત્રિકોણની ઊંચાઈ જેટલી છે. , જે આપણને અગાઉનું સૂત્ર આપે છે
• મનસ્વી ત્રિકોણનું ક્ષેત્રફળ શોધી શકાય છે દ્વારા કામવર્તુળની અડધી ત્રિજ્યા તેની બધી બાજુઓની લંબાઈના સરવાળા દ્વારા તેમાં અંકિત છે(સૂત્ર 3), સરળ રીતે કહીએ તો, તમારે ત્રિકોણની અર્ધ-પરિમિતિને અંકિત વર્તુળની ત્રિજ્યાથી ગુણાકાર કરવાની જરૂર છે (આ યાદ રાખવું વધુ સરળ છે)
• મનસ્વી ત્રિકોણનું ક્ષેત્રફળ તેની ચારે બાજુના વર્તુળની 4 ત્રિજ્યા દ્વારા તેની બધી બાજુઓના ગુણાંકને વિભાજીત કરીને શોધી શકાય છે (સૂત્ર 4)
• ફોર્મ્યુલા 5 ત્રિકોણનું ક્ષેત્રફળ તેની બાજુઓની લંબાઈ અને તેની અર્ધ પરિમિતિ (તેની બધી બાજુઓનો અડધો સરવાળો) દ્વારા શોધી રહ્યું છે.
• હેરોનનું સૂત્ર(6) અર્ધ-પરિમિતિના ખ્યાલનો ઉપયોગ કર્યા વિના, માત્ર બાજુઓની લંબાઈ દ્વારા સમાન સૂત્રનું પ્રતિનિધિત્વ છે
• મનસ્વી ત્રિકોણનું ક્ષેત્રફળ ત્રિકોણની બાજુના ચોરસના ગુણાંક જેટલું હોય છે અને આ બાજુને અડીને આવેલા ખૂણાઓની સાઈનને આ બાજુની સામેના ખૂણાની ડબલ સાઈન વડે ભાગવામાં આવે છે (સૂત્ર 7)
• મનસ્વી ત્રિકોણનું ક્ષેત્રફળ તેના પ્રત્યેક ખૂણાના સાઇન્સ દ્વારા તેની ફરતે ઘેરાયેલા વર્તુળના બે ચોરસના ગુણાંક તરીકે શોધી શકાય છે. (સૂત્ર 8)
• જો એક બાજુની લંબાઈ અને બે અડીને આવેલા ખૂણાઓની કિંમતો જાણીતી હોય, તો ત્રિકોણનો વિસ્તાર આ બાજુના ચોરસ તરીકે શોધી શકાય છે જે આ ખૂણાઓના કોટિન્જન્ટ્સના બેવડા સરવાળાથી ભાગવામાં આવે છે (સૂત્ર 9)
• જો ત્રિકોણની દરેક ઊંચાઈની માત્ર લંબાઈ જ જાણીતી હોય (સૂત્ર 10), તો આવા ત્રિકોણનું ક્ષેત્રફળ આ ઊંચાઈની લંબાઈના વિપરિત પ્રમાણસર હોય છે, જેમ કે હેરોનના સૂત્ર મુજબ
• ફોર્મ્યુલા 11 તમને ગણતરી કરવાની મંજૂરી આપે છે તેના શિરોબિંદુઓના કોઓર્ડિનેટ્સ પર આધારિત ત્રિકોણનો વિસ્તાર, જે દરેક શિરોબિંદુઓ માટે (x;y) મૂલ્યો તરીકે ઉલ્લેખિત છે. મહેરબાની કરીને નોંધ કરો કે પરિણામી મૂલ્ય મોડ્યુલો લેવું આવશ્યક છે, કારણ કે વ્યક્તિગત (અથવા તમામ) શિરોબિંદુઓના કોઓર્ડિનેટ્સ નકારાત્મક મૂલ્યોના ક્ષેત્રમાં હોઈ શકે છે.

નોંધ. ત્રિકોણનું ક્ષેત્રફળ શોધવા માટે ભૂમિતિની સમસ્યાઓ હલ કરવાના ઉદાહરણો નીચે આપેલા છે. જો તમારે ભૂમિતિની સમસ્યા હલ કરવાની જરૂર હોય જે અહીં સમાન નથી, તો ફોરમમાં તેના વિશે લખો. ઉકેલોમાં, "ચોરસમૂળ" પ્રતીકને બદલે, sqrt() ફંક્શનનો ઉપયોગ કરી શકાય છે, જેમાં sqrt એ વર્ગમૂળનું પ્રતીક છે, અને રેડિકન્ડ અભિવ્યક્તિ કૌંસમાં દર્શાવેલ છે..કેટલીકવાર સરળ આમૂલ અભિવ્યક્તિઓ માટે પ્રતીકનો ઉપયોગ કરી શકાય છે √

કાર્ય. બે બાજુઓ આપેલ વિસ્તાર અને તેમની વચ્ચેનો ખૂણો શોધો

ત્રિકોણની બાજુઓ 5 અને 6 સેમી છે તેમની વચ્ચેનો કોણ 60 ડિગ્રી છે. ત્રિકોણનું ક્ષેત્રફળ શોધો.

ઉકેલ.

આ સમસ્યાને ઉકેલવા માટે, અમે પાઠના સૈદ્ધાંતિક ભાગમાંથી સૂત્ર નંબર બેનો ઉપયોગ કરીએ છીએ.
ત્રિકોણનું ક્ષેત્રફળ બે બાજુઓની લંબાઈ અને તેમની વચ્ચેના કોણની સાઈન દ્વારા શોધી શકાય છે અને તે બરાબર હશે
S=1/2 ab sin γ

અમારી પાસે સોલ્યુશન માટેના તમામ જરૂરી ડેટા હોવાથી (સૂત્ર મુજબ), અમે માત્ર સમસ્યાની પરિસ્થિતિઓમાંથી મૂલ્યોને સૂત્રમાં બદલી શકીએ છીએ:
S = 1/2 * 5 * 6 * sin 60

મૂલ્યોના કોષ્ટકમાં ત્રિકોણમિતિ કાર્યોચાલો સાઈન 60 ડિગ્રીના મૂલ્યને અભિવ્યક્તિમાં શોધી અને બદલીએ. તે ત્રણ ગુણ્યા બે ના મૂળ સમાન હશે.
S = 15 √3 / 2

જવાબ આપો: 7.5 √3 (શિક્ષકની આવશ્યકતાઓને આધારે, તમે કદાચ 15 √3/2 છોડી શકો છો)

કાર્ય. સમભુજ ત્રિકોણનું ક્ષેત્રફળ શોધો

3 સેમી બાજુવાળા સમબાજુ ત્રિકોણનું ક્ષેત્રફળ શોધો.

ઉકેલ.

હેરોનના સૂત્રનો ઉપયોગ કરીને ત્રિકોણનું ક્ષેત્રફળ શોધી શકાય છે:

S = 1/4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))

a = b = c હોવાથી, સમભુજ ત્રિકોણના ક્ષેત્રફળ માટેનું સૂત્ર આ સ્વરૂપ લે છે:

S = √3 / 4 * a 2

S = √3 / 4 * 3 2

જવાબ આપો: 9 √3 / 4.

કાર્ય. બાજુઓની લંબાઈ બદલતી વખતે વિસ્તાર બદલો

જો બાજુઓને 4 ગણો વધારવામાં આવે તો ત્રિકોણનું ક્ષેત્રફળ કેટલી વાર વધશે?

ઉકેલ.

ત્રિકોણની બાજુઓના પરિમાણ આપણને અજાણ્યા હોવાથી, સમસ્યાના ઉકેલ માટે આપણે ધારીશું કે બાજુઓની લંબાઈ અનુક્રમે a, b, c ની મનસ્વી સંખ્યાઓ જેટલી છે. પછી, સમસ્યાના પ્રશ્નનો જવાબ આપવા માટે, આપણે આપેલ ત્રિકોણનો વિસ્તાર શોધીશું, અને પછી આપણે ત્રિકોણનો વિસ્તાર શોધીશું જેની બાજુઓ ચાર ગણી મોટી છે. આ ત્રિકોણના ક્ષેત્રોનો ગુણોત્તર આપણને સમસ્યાનો જવાબ આપશે.

નીચે અમે સમસ્યાના પગલા-દર-પગલાના ઉકેલની શાબ્દિક સમજૂતી આપીએ છીએ. જો કે, ખૂબ જ અંતે, આ જ ઉકેલ વધુ અનુકૂળ ગ્રાફિકલ સ્વરૂપમાં રજૂ કરવામાં આવ્યો છે. રસ ધરાવતા લોકો તરત જ ઉકેલો નીચે જઈ શકે છે.

ઉકેલવા માટે, અમે હેરોનના સૂત્રનો ઉપયોગ કરીએ છીએ (પાઠના સૈદ્ધાંતિક ભાગમાં ઉપર જુઓ). તે આના જેવું દેખાય છે:

S = 1/4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
(નીચે ચિત્રની પ્રથમ લીટી જુઓ)

મનસ્વી ત્રિકોણની બાજુઓની લંબાઈ a, b, c ચલ દ્વારા નિર્દિષ્ટ કરવામાં આવે છે.
જો બાજુઓને 4 ગણો વધારવામાં આવે, તો નવા ત્રિકોણ c નો વિસ્તાર હશે:

S 2 = 1/4 sqrt((4a + 4b + 4c)(4b + 4c - 4a)(4a + 4c - 4b)(4a + 4b -4c))
(નીચે ચિત્રમાં બીજી લીટી જુઓ)

જેમ તમે જોઈ શકો છો, 4 એ એક સામાન્ય પરિબળ છે જેને તમામ ચાર અભિવ્યક્તિઓમાંથી કૌંસમાંથી બહાર કાઢી શકાય છે. સામાન્ય નિયમોગણિત
પછી

S 2 = 1/4 sqrt(4 * 4 * 4 * 4 (a + b + c)(b + c - a)(a + c - b)(a + b -c)) - ચિત્રની ત્રીજી લાઇન પર
S 2 = 1/4 sqrt(256 (a + b + c)(b + c - a)(a + c - b)(a + b -c)) - ચોથી લીટી

256 નંબરનું વર્ગમૂળ સંપૂર્ણ રીતે કાઢવામાં આવ્યું છે, તો ચાલો તેને મૂળની નીચેથી બહાર કાઢીએ.
S 2 = 16 * 1/4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
S 2 = 4 sqrt((a + b + c)(b + c - a)(a + c - b)(a + b -c))
(નીચે ચિત્રની પાંચમી લાઇન જુઓ)

સમસ્યામાં પૂછાયેલા પ્રશ્નનો જવાબ આપવા માટે, આપણે ફક્ત પરિણામી ત્રિકોણના ક્ષેત્રફળને મૂળ ત્રિકોણના ક્ષેત્રફળ દ્વારા વિભાજીત કરવાની જરૂર છે.
ચાલો એકબીજા દ્વારા સમીકરણોને વિભાજીત કરીને અને પરિણામી અપૂર્ણાંકને ઘટાડીને વિસ્તાર ગુણોત્તર નક્કી કરીએ.