Determina el área del triángulo basándose en tres lados. Cómo encontrar el área de un triángulo

Concepto de área

El concepto de área de cualquier figura geométrica, en particular un triángulo, estará asociado a una figura como un cuadrado. Para la unidad de área de cualquier figura geométrica tomaremos el área de un cuadrado cuyo lado es igual a uno. Para completar, recordemos dos propiedades básicas del concepto de áreas. formas geométricas.

Propiedad 1: Si las figuras geométricas son iguales, entonces sus áreas también lo son.

Propiedad 2: Cualquier figura se puede dividir en varias figuras. Además, el área de la figura original es igual a la suma de las áreas de todas sus figuras constituyentes.

Veamos un ejemplo.

Ejemplo 1

Obviamente, uno de los lados del triángulo es una diagonal de un rectángulo, un lado del cual tiene una longitud de $5$ (ya que hay $5$ celdas) y el otro es $6$ (ya que hay $6$ celdas). Por tanto, el área de este triángulo será igual a la mitad de dicho rectángulo. El área del rectángulo es

Entonces el área del triángulo es igual a

Respuesta: $15$.

A continuación, consideraremos varios métodos para encontrar las áreas de triángulos, es decir, usando la altura y la base, usando la fórmula de Heron y el área de un triángulo equilátero.

Cómo encontrar el área de un triángulo usando su altura y base

Teorema 1

El área de un triángulo se puede encontrar como la mitad del producto de la longitud de un lado por la altura de ese lado.

Matemáticamente se ve así

$S=\frac(1)(2)αh$

donde $a$ es la longitud del lado, $h$ es la altura dibujada hacia él.

Prueba.

Considere un triángulo $ABC$ en el que $AC=α$. Hacia este lado se dibuja la altura $BH$, que es igual a $h$. Vamos a construirlo hasta el cuadrado $AXYC$ como en la Figura 2.

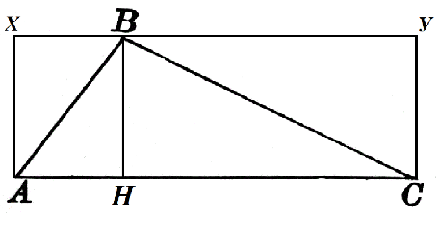
El área del rectángulo $AXBH$ es $h\cdot AH$, y el área del rectángulo $HBYC$ es $h\cdot HC$. Entonces

$S_ABH=\frac(1)(2)h\cdot AH$, $S_CBH=\frac(1)(2)h\cdot HC$

Por tanto, el área requerida del triángulo, según la propiedad 2, es igual a

$S=S_ABH+S_CBH=\frac(1)(2)h\cdot AH+\frac(1)(2)h\cdot HC=\frac(1)(2)h\cdot (AH+HC)=\ frac(1)(2)αh$

El teorema ha sido demostrado.

Ejemplo 2

Encuentra el área del triángulo en la siguiente figura si la celda tiene un área igual a uno

La base de este triángulo es igual a $9$ (ya que $9$ son $9$ cuadrados). La altura también es $9$. Entonces, por el teorema 1, obtenemos

$S=\frac(1)(2)\cdot 9\cdot 9=40.5$

Respuesta: $40,5$.

la fórmula de garza

Teorema 2

Si nos dan tres lados de un triángulo $α$, $β$ y $γ$, entonces su área se puede encontrar de la siguiente manera

$S=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

aquí $ρ$ significa el semiperímetro de este triángulo.

Prueba.

Considere la siguiente figura:

Por el teorema de Pitágoras, del triángulo $ABH$ obtenemos

Del triángulo $CBH$, según el teorema de Pitágoras, tenemos

$h^2=α^2-(β-x)^2$

$h^2=α^2-β^2+2βxx^2$

De estas dos relaciones obtenemos la igualdad

$γ^2-x^2=α^2-β^2+2βx-x^2$

$x=\frac(γ^2-α^2+β^2)(2β)$

$h^2=γ^2-(\frac(γ^2-α^2+β^2)(2β))^2$

$h^2=\frac((α^2-(γ-β)^2)((γ+β)^2-α^2))(4β^2)$

$h^2=\frac((α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α))(4β^2)$

Dado que $ρ=\frac(α+β+γ)(2)$, entonces $α+β+γ=2ρ$, lo que significa

$h^2=\frac(2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α))(4β^2)$

$h^2=\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2 )$

$h=\sqrt(\frac(4ρ(ρ-α)(ρ-β)(ρ-γ))(β^2))$

$h=\frac(2)(β)\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

Por el teorema 1, obtenemos

$S=\frac(1)(2) βh=\frac(β)(2)\cdot \frac(2)(β) \sqrt(ρ(ρ-α)(ρ-β)(ρ-γ) )=\sqrt(ρ(ρ-α)(ρ-β)(ρ-γ))$

Del vértice opuesto) y divide el producto resultante entre dos. Esto se parece a esto:

S = ½ * a * h,

Dónde:
S – área del triángulo,
a es la longitud de su lado,
h es la altura bajada a este lado.

La longitud y la altura de los lados deben presentarse en las mismas unidades de medida. En este caso el área del triángulo se obtendrá en las unidades “ ” correspondientes.

Ejemplo.
En un lado de un triángulo escaleno de 20 cm de largo, se baja una perpendicular desde el vértice opuesto de 10 cm de largo.
Se requiere el área del triángulo.
Solución.
S = ½ * 20 * 10 = 100 (cm²).

Si se conocen las longitudes de dos lados cualesquiera de un triángulo escaleno y el ángulo entre ellos, entonces use la fórmula:

S = ½ * a * b * senγ,

donde: a, b son las longitudes de dos lados arbitrarios y γ es el ángulo entre ellos.

En la práctica, por ejemplo, al medir terrenos, el uso de las fórmulas anteriores a veces es difícil, ya que requiere construcción y medición de ángulos adicionales.

Si conoces las longitudes de los tres lados de un triángulo escaleno, usa la fórmula de Heron:

S = √(p(p-a)(pb)(p-c)),

a, b, c – longitudes de los lados del triángulo,
p – semiperímetro: p = (a+b+c)/2.

Si, además de las longitudes de todos los lados, se conoce el radio del círculo inscrito en el triángulo, se utiliza la siguiente fórmula compacta:

donde: r – radio del círculo inscrito (р – semiperímetro).

Para calcular el área de un triángulo escaleno y la longitud de sus lados, use la fórmula:

donde: R – radio del círculo circunscrito.

Si conoce la longitud de uno de los lados del triángulo y tres ángulos (en principio, dos son suficientes; el valor del tercero se calcula a partir de la igualdad de la suma de los tres ángulos del triángulo - 180º), entonces use la formula:

S = (a² * sinβ * sinγ)/2sinα,

donde α es el valor del ángulo opuesto al lado a;
β, γ – valores de los dos ángulos restantes del triángulo.

La necesidad de encontrar varios elementos, incluido el área. triángulo, apareció muchos siglos antes de Cristo entre los astrónomos eruditos. Antigua Grecia. Cuadrado triángulo se puede calcular diferentes caminos utilizando diferentes fórmulas. El método de cálculo depende de qué elementos triángulo conocido.

Instrucciones

Si de la condición conocemos los valores de dos lados b, c y el ángulo que forman ellos?, entonces el área triángulo ABC se encuentra mediante la fórmula:
S = (bcsen?)/2.

Si de la condición conocemos los valores de dos lados a, b y el ángulo que no forman ellos?, entonces el área triángulo ABC se encuentra de la siguiente manera:
¿Encontrar el ángulo?, ¿pecado? = bsen?/a, luego usa la tabla para determinar el ángulo en sí.
¿Encontrar el ángulo?, ? = 180°-?-?.
Encontramos el área misma S = (absin?)/2.

Si de la condición conocemos los valores de solo tres lados triángulo a, b y c, entonces el área triángulo ABC se encuentra mediante la fórmula:
S = v(p(p-a)(p-b)(p-c)) , donde p es el semiperímetro p = (a+b+c)/2

Si por las condiciones del problema conocemos la altura triángulo h y el lado al que se baja esta altura, entonces el área triángulo ABC según la fórmula:
S = ah(a)/2 = bh(b)/2 = ch(c)/2.

Si conocemos el significado de los lados triángulo a, b, c y el radio descrito sobre este triángulo R, entonces el área de este triángulo ABC está determinado por la fórmula:
S = abc/4R.
Si se conocen tres lados a, b, c y el radio del inscrito, entonces el área triángulo ABC se encuentra mediante la fórmula:
S = pr, donde p es el semiperímetro, p = (a+b+c)/2.

Si ABC es equilátero, entonces el área se encuentra mediante la fórmula:
S = (a^2v3)/4.
Si el triángulo ABC es isósceles, entonces el área está determinada por la fórmula:
S = (cv(4a^2-c^2))/4, donde c – triángulo.
Si el triángulo ABC es rectángulo, entonces el área está determinada por la fórmula:
S = ab/2, donde a y b son catetos triángulo.
Si el triángulo ABC es un triángulo rectángulo isósceles, entonces el área está determinada por la fórmula:
S = c^2/4 = a^2/2, donde c es la hipotenusa triángulo, a=b – pierna.

Vídeo sobre el tema.

Fuentes:

cómo medir el área de un triángulo

Consejo 3: Cómo encontrar el área de un triángulo si se conoce el ángulo

Conocer un solo parámetro (el ángulo) no es suficiente para encontrar el área tre cuadrado . Si hay dimensiones adicionales, para determinar el área se puede elegir una de las fórmulas en las que también se utiliza el valor del ángulo como una de las variables conocidas. A continuación se detallan varias de las fórmulas más utilizadas.

Instrucciones

Si además del tamaño del ángulo (γ) formado por los dos lados tre cuadrado , las longitudes de estos lados (A y B) también son conocidas, entonces cuadrado(S) de una figura se puede definir como la mitad del producto de las longitudes de los lados y el seno de este ángulo conocido: S=½×A×B×sin(γ).

Como recordarás de currículum escolar Según la geometría, un triángulo es una figura formada por tres segmentos conectados por tres puntos que no se encuentran en la misma línea recta. Un triángulo forma tres ángulos, de ahí el nombre de la figura. La definición puede ser diferente. Un triángulo también se puede llamar polígono de tres ángulos, la respuesta también será correcta. Los triángulos se dividen según el número de lados iguales y el tamaño de los ángulos en las figuras. Así, los triángulos se distinguen en isósceles, equiláteros y escalenos, además de rectangulares, agudos y obtusos, respectivamente.

Existen muchas fórmulas para calcular el área de un triángulo. Elige cómo encontrar el área de un triángulo, es decir Depende de usted qué fórmula utilizar. Pero vale la pena señalar solo algunas de las notaciones que se utilizan en muchas fórmulas para calcular el área de un triángulo. Así que recuerda:

S es el área del triángulo,

a, b, c son los lados del triángulo,

h es la altura del triángulo,

R es el radio del círculo circunscrito,

p es el semiperímetro.

Aquí están las notaciones básicas que pueden resultarle útiles si olvidó por completo su curso de geometría. A continuación se muestran las opciones más comprensibles y sencillas para calcular el área desconocida y misteriosa de un triángulo. No es difícil y te será útil tanto para las necesidades de tu hogar como para ayudar a tus hijos. Recordemos cómo calcular el área de un triángulo de la forma más sencilla posible:

En nuestro caso, el área del triángulo es: S = ½ * 2,2 cm * 2,5 cm = 2,75 cm cuadrados. Recuerda que el área se mide en centímetros cuadrados (sqcm).

Triángulo rectángulo y su área.

Un triángulo rectángulo es un triángulo en el que un ángulo mide 90 grados (de ahí que se le llame recto). Un ángulo recto está formado por dos rectas perpendiculares (en el caso de un triángulo, dos segmentos perpendiculares). EN triángulo rectángulo Sólo puede haber un ángulo recto, porque la suma de todos los ángulos de cualquier triángulo es igual a 180 grados. Resulta que otros 2 ángulos deben dividir los 90 grados restantes, por ejemplo 70 y 20, 45 y 45, etc. Entonces, recuerdas lo principal, solo queda descubrir cómo encontrar el área de un triángulo rectángulo. Imaginemos que tenemos un triángulo rectángulo frente a nosotros y necesitamos encontrar su área S.

1. La forma más sencilla de determinar el área de un triángulo rectángulo se calcula mediante la siguiente fórmula:

En nuestro caso, el área del triángulo rectángulo es: S = 2,5 cm * 3 cm / 2 = 3,75 cm cuadrados.

En principio, ya no es necesario verificar el área del triángulo de otras formas, porque Sólo éste será útil y ayudará en la vida cotidiana. Pero también existen opciones para medir el área de un triángulo a través de ángulos agudos.

2. Para otros métodos de cálculo, es necesario disponer de una tabla de cosenos, senos y tangentes. Juzgue usted mismo, aquí hay algunas opciones para calcular el área de un triángulo rectángulo que aún se pueden usar:

Decidimos usar la primera fórmula y con algunos borrones menores (la dibujamos en un cuaderno y usamos una regla y un transportador viejos), pero obtuvimos el cálculo correcto:

S = (2,5*2,5)/(2*0,9)=(3*3)/(2*1,2). Obtuvimos los siguientes resultados: 3,6=3,7, pero teniendo en cuenta el desplazamiento de las células, podemos perdonar este matiz.

Triángulo isósceles y su área.

Si se enfrenta a la tarea de calcular la fórmula de un triángulo isósceles, entonces la forma más sencilla es utilizar la fórmula principal y la que se considera clásica para el área de un triángulo.

Pero primero, antes de encontrar el área de un triángulo isósceles, averigüemos qué tipo de figura es. Un triángulo isósceles es un triángulo en el que dos lados tienen la misma longitud. Estos dos lados se llaman laterales, el tercer lado se llama base. No confundas un triángulo isósceles con un triángulo equilátero, es decir un triángulo regular con los tres lados iguales. En tal triángulo no hay tendencias especiales en los ángulos, o más bien en su tamaño. Sin embargo, los ángulos en la base de un triángulo isósceles son iguales, pero diferentes del ángulo entre lados iguales. Entonces, ya conoces la primera y principal fórmula, queda por descubrir qué otras fórmulas para determinar el área de un triángulo isósceles se conocen:

El triángulo es una de las formas geométricas más comunes, que ya conocemos en escuela primaria. Cada estudiante se enfrenta a la pregunta de cómo encontrar el área de un triángulo en las lecciones de geometría. Entonces, ¿qué características se pueden identificar al encontrar el área de una figura determinada? En este artículo veremos las fórmulas básicas necesarias para realizar dicha tarea y también analizaremos los tipos de triángulos.

tipos de triangulos

Puedes encontrar el área de un triángulo en forma absoluta. diferentes caminos, porque en geometría hay más de un tipo de figuras que contienen tres ángulos. Estos tipos incluyen:

Obtuso.
Equilátero (correcto).
Triángulo rectángulo.
Isósceles.

Echemos un vistazo más de cerca a cada uno de ellos. tipos existentes triangulos.

Esta figura geométrica se considera la más común a la hora de resolver problemas geométricos. Cuando surge la necesidad de dibujar un triángulo arbitrario, esta opción viene al rescate.

En un triángulo agudo, como su nombre indica, todos los ángulos son agudos y suman 180°.

Este tipo de triángulo también es muy común, pero algo menos común que un triángulo agudo. Por ejemplo, al resolver triángulos (es decir, se conocen varios de sus lados y ángulos y es necesario encontrar los elementos restantes), a veces es necesario determinar si el ángulo es obtuso o no. El coseno es un número negativo.

B, el valor de uno de los ángulos supera los 90°, por lo que los dos ángulos restantes pueden tomar valores pequeños (por ejemplo, 15° o incluso 3°).

Para encontrar el área de un triángulo de este tipo es necesario conocer algunos matices, de los que hablaremos más adelante.

Triángulos regulares e isósceles

Un polígono regular es una figura que incluye n ángulos y cuyos lados y ángulos son todos iguales. Esto es lo que es un triángulo regular. Como la suma de todos los ángulos de un triángulo es 180°, entonces cada uno de los tres ángulos mide 60°.

Un triángulo regular, por su propiedad, también se llama figura equilátera.

También vale la pena señalar que en un triángulo regular solo se puede inscribir un círculo, y alrededor de él solo se puede describir un círculo, y sus centros están ubicados en el mismo punto.

Además del tipo equilátero, también se puede distinguir un triángulo isósceles, que se diferencia ligeramente de él. En tal triángulo, dos lados y dos ángulos son iguales entre sí, y el tercer lado (al que son adyacentes ángulos iguales) es la base.

La figura muestra un triángulo isósceles DEF cuyos ángulos D y F son iguales y DF es la base.

Triángulo rectángulo

Un triángulo rectángulo se llama así porque uno de sus ángulos es recto, es decir, igual a 90°. Los otros dos ángulos suman 90°.

El lado más grande de dicho triángulo, opuesto al ángulo de 90°, es la hipotenusa, mientras que los dos lados restantes son los catetos. Para este tipo de triángulo se aplica el teorema de Pitágoras:

La suma de los cuadrados de las longitudes de los catetos es igual al cuadrado de la longitud de la hipotenusa.

La figura muestra un triángulo rectángulo BAC con hipotenusa AC y catetos AB y BC.

Para encontrar el área de un triángulo con ángulo recto, necesitas conocer los valores numéricos de sus catetos.

Pasemos a las fórmulas para encontrar el área de una figura determinada.

Fórmulas básicas para encontrar el área.

En geometría, se pueden distinguir dos fórmulas que son adecuadas para encontrar el área de la mayoría de los tipos de triángulos, a saber, agudos, obtusos, regulares y triángulos isósceles. Veamos cada uno de ellos.

Por lado y altura

Esta fórmula es universal para encontrar el área de la figura que estamos considerando. Para hacer esto, basta con conocer la longitud del lado y la longitud de la altura dibujada hacia él. La fórmula en sí (la mitad del producto de la base por la altura) es la siguiente:

donde A es el lado de un triángulo dado y H es la altura del triángulo.

Por ejemplo, para encontrar el área de un triángulo agudo ACB, debes multiplicar su lado AB por la altura CD y dividir el valor resultante por dos.

Sin embargo, no siempre es fácil encontrar el área de un triángulo de esta forma. Por ejemplo, para usar esta fórmula para un triángulo obtuso, debes extender uno de sus lados y solo entonces dibujarle una altura.

En la práctica, esta fórmula se utiliza con más frecuencia que otras.

En ambos lados y esquina

Esta fórmula, como la anterior, es adecuada para la mayoría de los triángulos y en su significado es consecuencia de la fórmula para encontrar el área por lado y la altura de un triángulo. Es decir, la fórmula en cuestión se puede derivar fácilmente de la anterior. Su formulación queda así:

S = ½*senO*A*B,

donde A y B son los lados del triángulo y O es el ángulo entre los lados A y B.

Recordemos que el seno de un ángulo se puede consultar en una tabla especial que lleva el nombre del destacado matemático soviético V. M. Bradis.

Pasemos ahora a otras fórmulas que solo son adecuadas para tipos excepcionales de triángulos.

Área de un triángulo rectángulo

Además de la fórmula universal, que incluye la necesidad de encontrar la altura en un triángulo, el área de un triángulo que contiene un ángulo recto se puede encontrar a partir de sus catetos.

Por tanto, el área de un triángulo que contiene un ángulo recto es la mitad del producto de sus catetos, o:

donde a y b son los catetos de un triángulo rectángulo.

Triángulo regular

Este tipo figuras geométricas se diferencia en que su área se puede encontrar con el valor indicado de solo uno de sus lados (ya que todos los lados de un triángulo regular son iguales). Entonces, ante la tarea de "encontrar el área de un triángulo cuando los lados son iguales", debes usar la siguiente fórmula:

S = Un 2 *√3 / 4,

donde A es el lado del triángulo equilátero.

la fórmula de garza

La última opción para encontrar el área de un triángulo es la fórmula de Heron. Para poder utilizarlo es necesario conocer las longitudes de los tres lados de la figura. La fórmula de Heron se ve así:

S = √p·(p - a)·(p - b)·(p - c),

donde a, b y c son los lados de un triángulo dado.

A veces se da el problema: “el área de un triángulo regular es encontrar la longitud de su lado”. EN en este caso Necesitamos usar la fórmula que ya conocemos para encontrar el área de un triángulo regular y derivar de ella el valor del lado (o su cuadrado):

Un 2 = 4S / √3.

Tareas de examen

Hay muchas fórmulas en los problemas GIA en matemáticas. Además, muy a menudo es necesario encontrar el área de un triángulo en papel cuadriculado.

En este caso, lo más conveniente es dibujar la altura a uno de los lados de la figura, determinar su longitud a partir de las celdas y usar fórmula universal para encontrar el área:

Entonces, después de estudiar las fórmulas presentadas en el artículo, no tendrás problemas para encontrar el área de un triángulo de cualquier tipo.

Área de un triángulo: fórmulas y ejemplos de resolución de problemas

Debajo están fórmulas para encontrar el área de un triángulo arbitrario los cuales son adecuados para encontrar el área de cualquier triángulo, independientemente de sus propiedades, ángulos o tamaños. Las fórmulas se presentan en forma de imagen, con explicaciones de su aplicación o justificación de su corrección. Además, una figura separada muestra la correspondencia entre los símbolos de letras en las fórmulas y los símbolos gráficos en el dibujo.

Nota . Si el triángulo tiene propiedades especiales (isosceles, rectangular, equilátero), puede utilizar las fórmulas que se indican a continuación, así como fórmulas especiales adicionales que son válidas sólo para triángulos con estas propiedades:

"Fórmula para el área de un triángulo equilátero"

Fórmulas de área de triángulo

Explicaciones de fórmulas:
a B C- las longitudes de los lados del triángulo cuya área queremos encontrar
r- radio del círculo inscrito en el triángulo
R- radio del círculo circunscrito alrededor del triángulo
h- altura del triángulo bajado hacia un lado
pag- semiperímetro de un triángulo, la mitad de la suma de sus lados (perímetro)
α - ángulo opuesto al lado a del triángulo
β - ángulo opuesto al lado b del triángulo
γ - ángulo opuesto al lado c del triángulo
h a, h b , h C- altura del triángulo bajada a los lados a, b, c

Tenga en cuenta que las notaciones dadas corresponden a la figura anterior, por lo que al resolver un problema de geometría real, le resultará visualmente más fácil sustituir los valores correctos en los lugares correctos de la fórmula.

El área del triángulo es la mitad del producto de la altura del triángulo por la longitud del lado por el cual se baja esta altura(Fórmula 1). La exactitud de esta fórmula se puede entender lógicamente. La altura bajada a la base dividirá un triángulo arbitrario en dos rectangulares. Si construyes cada uno de ellos en un rectángulo con dimensiones b y h, entonces obviamente el área de estos triángulos será igual a exactamente la mitad del área del rectángulo (Spr = bh)
El área del triángulo es la mitad del producto de sus dos lados por el seno del ángulo entre ellos(Fórmula 2) (vea un ejemplo de cómo resolver un problema usando esta fórmula a continuación). Aunque parezca diferente al anterior, se puede transformar fácilmente en él. Si bajamos la altura del ángulo B al lado b, resulta que el producto del lado a por el seno del ángulo γ, según las propiedades del seno en un triángulo rectángulo, es igual a la altura del triángulo que dibujamos. , que nos da la fórmula anterior
Se puede encontrar el área de un triángulo arbitrario. a través de trabajar la mitad del radio del círculo inscrito en él por la suma de las longitudes de todos sus lados(Fórmula 3), en pocas palabras, debes multiplicar el semiperímetro del triángulo por el radio del círculo inscrito (esto es más fácil de recordar)
El área de un triángulo arbitrario se puede encontrar dividiendo el producto de todos sus lados por 4 radios del círculo circunscrito a su alrededor (Fórmula 4)
La fórmula 5 consiste en encontrar el área de un triángulo a través de las longitudes de sus lados y su semiperímetro (la mitad de la suma de todos sus lados)
la fórmula de garza(6) es una representación de la misma fórmula sin utilizar el concepto de semiperímetro, sólo a través de las longitudes de los lados
El área de un triángulo arbitrario es igual al producto del cuadrado del lado del triángulo y los senos de los ángulos adyacentes a este lado dividido por el doble seno del ángulo opuesto a este lado (Fórmula 7)
El área de un triángulo arbitrario se puede encontrar como el producto de dos cuadrados del círculo circunscrito a él por los senos de cada uno de sus ángulos. (Fórmula 8)
Si se conocen la longitud de un lado y los valores de dos ángulos adyacentes, entonces el área del triángulo se puede encontrar como el cuadrado de este lado dividido por la doble suma de las cotangentes de estos ángulos (Fórmula 9)
Si solo se conoce la longitud de cada una de las alturas del triángulo (Fórmula 10), entonces el área de dicho triángulo es inversamente proporcional a las longitudes de estas alturas, como según la Fórmula de Heron
La fórmula 11 te permite calcular. área de un triángulo según las coordenadas de sus vértices, que se especifican como valores (x;y) para cada uno de los vértices. Tenga en cuenta que el valor resultante debe tomarse en módulo, ya que las coordenadas de los vértices individuales (o incluso de todos) pueden estar en la región de valores negativos.

Nota. Los siguientes son ejemplos de resolución de problemas de geometría para encontrar el área de un triángulo. Si necesitas resolver un problema de geometría que no es similar aquí, escríbelo en el foro. En las soluciones, en lugar del símbolo de "raíz cuadrada", se puede utilizar la función sqrt(), en la que sqrt es el símbolo de la raíz cuadrada y la expresión radical se indica entre paréntesis..A veces, para expresiones radicales simples, se puede utilizar el símbolo. √

Tarea. Calcula el área dados dos lados y el ángulo entre ellos.

Los lados del triángulo miden 5 y 6 cm. El ángulo entre ellos es de 60 grados. Encuentra el área del triángulo..

Solución.

Para solucionar este problema utilizamos la fórmula número dos de la parte teórica de la lección.
El área de un triángulo se puede encontrar a través de las longitudes de dos lados y el seno del ángulo entre ellos y será igual a
S=1/2 ab sen γ

Como tenemos todos los datos necesarios para la solución (según la fórmula), solo podemos sustituir los valores de las condiciones del problema en la fórmula:
S = 1/2 * 5 * 6 * pecado 60

En la tabla de valores funciones trigonométricas Busquemos y sustituyamos el valor del seno de 60 grados en la expresión. Será igual a la raíz de tres por dos.
S = 15 √3 / 2

Respuesta: 7.5 √3 (dependiendo de los requerimientos del profesor, probablemente puedas dejar 15 √3/2)

Tarea. Encuentra el área de un triángulo equilátero

Calcula el área de un triángulo equilátero de 3 cm de lado.

Solución .

El área de un triángulo se puede encontrar usando la fórmula de Heron:

S = 1/4 raíz cuadrada ((a + b + c)(b + c - a)(a + c - b)(a + b -c))

Como a = b = c, la fórmula para el área de un triángulo equilátero toma la forma:

S = √3 / 4 * a 2

S = √3 / 4 * 3 2

Respuesta: 9 √3 / 4.

Tarea. Cambio de área al cambiar la longitud de los lados

¿Cuántas veces aumentará el área del triángulo si los lados aumentan 4 veces?

Solución.

Dado que desconocemos las dimensiones de los lados del triángulo, para resolver el problema asumiremos que las longitudes de los lados son respectivamente iguales a los números arbitrarios a, b, c. Luego, para responder a la pregunta del problema, encontraremos el área del triángulo dado, y luego encontraremos el área del triángulo cuyos lados son cuatro veces más grandes. La razón de las áreas de estos triángulos nos dará la respuesta al problema.

A continuación proporcionamos una explicación textual de la solución al problema paso a paso. Sin embargo, al final, esta misma solución se presenta en una forma gráfica más conveniente. Los interesados pueden consultar inmediatamente las soluciones.

Para resolverlo utilizamos la fórmula de Heron (ver arriba en la parte teórica de la lección). Se parece a esto:

S = 1/4 raíz cuadrada ((a + b + c)(b + c - a)(a + c - b)(a + b -c))
(ver la primera línea de la imagen a continuación)

Las longitudes de los lados de un triángulo arbitrario están especificadas por las variables a, b, c.
Si los lados se aumentan 4 veces, entonces el área del nuevo triángulo c será:

S 2 = 1/4 raíz((4a + 4b + 4c)(4b + 4c - 4a)(4a + 4c - 4b)(4a + 4b -4c))
(ver segunda línea en la imagen de abajo)

Como puede ver, 4 es un factor común que se puede sacar entre paréntesis de las cuatro expresiones según reglas generales matemáticas.
Entonces

S 2 = 1/4 raíz cuadrada (4 * 4 * 4 * 4 (a + b + c)(b + c - a)(a + c - b)(a + b -c)) - en la tercera línea de la imagen
S 2 = 1/4 sqrt(256 (a + b + c)(b + c - a)(a + c - b)(a + b -c)) - cuarta linea

La raíz cuadrada del número 256 está perfectamente extraída, así que saquémosla de debajo de la raíz.
S 2 = 16 * 1/4 raíz cuadrada ((a + b + c)(b + c - a)(a + c - b)(a + b -c))
S 2 = 4 raíz cuadrada ((a + b + c)(b + c - a)(a + c - b)(a + b -c))
(ver quinta línea de la imagen a continuación)

Para responder a la pregunta del problema, solo necesitamos dividir el área del triángulo resultante por el área del original.
Determinemos las razones de área dividiendo las expresiones entre sí y reduciendo la fracción resultante.